
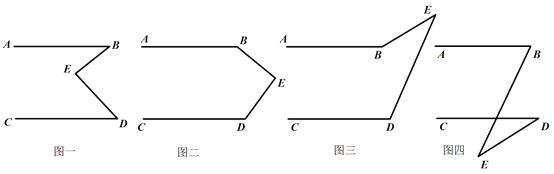
【题目】有一天李明同学用“几何画板”画图,他先画了两条平行线AB,CD,然后在平行线间画了一点E,连接BE,DE后(如图一),他用鼠标左键点住点E,拖动后,分别得到如图二,三,四等图形,这时他突然一想,∠B,∠D与∠BED之间的度数有没有某种联系呢?接着李明同学通过利用“几何画板”的“度量角度”和“计算”功能,找到了这三个角之间的关系.
(1)你能探究出图一到图四各图中的∠B,∠D与∠BED之间的关系吗?
(2)请从所得的四个关系中,选一个说明它成立的理由.
【答案】
如图,
(1)①∠B+∠D=∠BED;
②∠B+∠D+∠BED=360°;
③∠BED=∠D-∠B;
④∠BED=∠B-∠D;
(2)选图③.
过点E作EF∥AB,∵AB∥CD,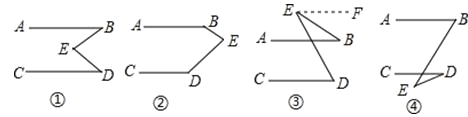
∴EF∥CD,
∴∠D=∠DEF,∠B=∠BEF,
又∵∠BED=∠DEF-∠BEF,
∴∠BED=∠D-∠B.
“点睛”本题考查了平行线的性质,此类题目解题关键在于过拐点作平行线.
【解析】(1)根据两直线平行,内错角相等,两直线平行解答;
(2)选择③,过点E作EF∥AB,根据两直线平行,内错角相等可得∠D=∠DEF,∠B=∠BEF,再根据∠BED=∠DEF-∠BEF整理即可得证.
解:如图,
(1)①∠B+∠D=∠BED;
②∠B+∠D+∠BED=360°;
③∠BED=∠D-∠B;
④∠BED=∠B-∠D;
(2)选图③.
过点E作EF∥AB,∵AB∥CD,
∴EF∥CD,
∴∠D=∠DEF,∠B=∠BEF,
又∵∠BED=∠DEF-∠BEF,
∴∠BED=∠D-∠B.


科目:初中数学 来源: 题型:
【题目】若三条线段的比是①1:4:6;②1:2:3,;③3:3:6;④6:6:10;⑤3:4:5;其中可构成三角形的有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列计算中,不能用平方差公式计算的是( )
A. (m-n)(-m+n) B. (x3-y3)(x3+y3)
C. (-a-b)(a-b) D. (c2–d2)(d2+c2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,是一张直角三角形的纸片,两直角边AC=6㎝,BC=8㎝,现将△ABC折叠,使点B与点A重合,折痕为DE,则AD的长为( )
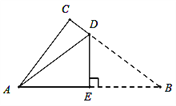
A. 4㎝ B. 5㎝ C. 6㎝ D. ![]() ㎝
㎝
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com