Question

7．已知抛物线C₁：y=ax²+bx+c经过点A（-1，0），B（3，0），C（0，-3）
（1）求抛物线C₁的解析式；
（2）将抛物线C₁向左平移几个单位长度，可使所得的抛物线C₂经过坐标原点，并写出C₂的解析式．

Answer 1

分析 （1）由于已知抛物线与x的两交点坐标，则可设交点式y=a（x+1）（x-3），然后把C（0，-3）代入求出a的值即可．
（2）求出原函数的图象对称轴，然后运用平移知识解答．

解答 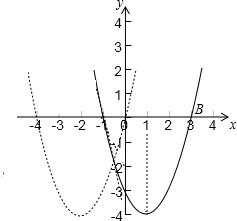解：（1）设抛物线解析式为y=a（x+1）（x-3），
把C（0，-3）代入得a•1•（-3）=-3，解得a=1，
所以抛物线解析式为y=（x+1）（x-3），即y=x²-2x-3．

（2）抛物线C₁向左平移3个单位长度，可使得到的抛物线C₂经过坐标原点．
所求抛物线C₂的解析式为：y=x（x+4）=x²+4x．

点评 本题主要考查待定系数求二次函数的解析式、二次函数图象与几何变换，根据题干条件解出函数解析式是解答本题的关键，此题难度不是很大．