
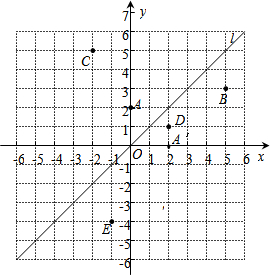
 如图,在平面直角坐标系中,直线l的解析式是y=x.
如图,在平面直角坐标系中,直线l的解析式是y=x. (解:(1)如图:B'(3,5),C'(5,-2);
(解:(1)如图:B'(3,5),C'(5,-2);
|
|
|
|
| 1 |
| 2 |
| 1 |
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
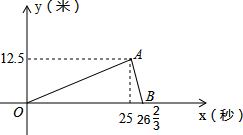 关冠与吉季代表我校参加田径运动会200米比赛,并分别获得冠军和季军,如图显示了赛程中的部分信息,用y表示两位同学的在比赛中的路程差,x表示时间(设速度均为匀速).
关冠与吉季代表我校参加田径运动会200米比赛,并分别获得冠军和季军,如图显示了赛程中的部分信息,用y表示两位同学的在比赛中的路程差,x表示时间(设速度均为匀速).查看答案和解析>>
科目:初中数学 来源: 题型:
| 价格 种类 | 进价 (元/台) | 售价 (元/台) |
| 电视机 | 5000 | 5480 |
| 洗衣机 | 2000 | 2280 |
| 空 调 | 2500 | 2800 |
查看答案和解析>>
科目:初中数学 来源: 题型:
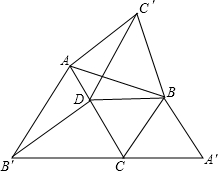 如图,在△ABC中,已知∠DBC=60°,AC>BC,又△ABC′、△BCA′、△CAB′都是△ABC形外的等边三角形,而点D在AC上,且BC=DC
如图,在△ABC中,已知∠DBC=60°,AC>BC,又△ABC′、△BCA′、△CAB′都是△ABC形外的等边三角形,而点D在AC上,且BC=DC查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com