
����Ŀ��ij���мס������ֳ�������ǵķ���������ͬ���ļƼ۷�ʽΪ������ʻ·�̲�����3ǧ��ʱ�շ�10Ԫ��ÿ����1ǧ���������շ�1.2Ԫ������1ǧ�װ�1ǧ���շѣ����ҵļƼ۷�ʽΪ������ʻ·�̲�����3ǧ��ʱ�շ�8Ԫ��ÿ����1ǧ���������շ�1.8Ԫ������1ǧ�װ�1ǧ���շѣ���ij�˵����г����Ҫ������·��Ϊxǧ�ף�
��1����x=5ʱ����ֱ���������ס������ֳ���ķ��ã�
��2���ô���ʽ��ʾ���˷ֱ�����ס��ҳ��������Ҫ�ķ��ã�
��3��������˳�����·��Ϊ13ǧ��һ�㣬�������������ֳ��Ϻ��㣿
���𰸡�
��1���⣺��x=5ʱ���ķ���=10+��5��3����1.2=10+2.4=12.4��Ԫ����
�ҵķ���=8+��5��3����1.8=8+3.6=11.6��Ԫ����
�𣺳����ס������ֳ���ķ��÷ֱ�Ϊ12.4Ԫ��11.6Ԫ
��2���⣺�ķ��� ![]() ��
��
�ҵķ��� ![]()
��3���⣺�ߴ��˳�����·��Ϊ13ǧ��һ�㣬
��x=14��
�ķ���10+1.2��14��3��=10+13.2=23.2��Ԫ����
�ҵķ���8+1.8��14��3��=8+19.8=27.8��Ԫ����
��23.2��27.8��
���������׳��������
����������1�����ݼ������ֳ���ļƼ۷�ʽ�ֱ���ʽ���㼴�ɵý⣻��2������x��3��x��3���������ʽ��ʾ���ɣ���3����x=14�ֱ�������ʽ���㼴�ɵý⣮
�����㾫����������Ŀ����֪���������ô���ʽ��ֵ�����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���������ʽ��ֵ��һ�����Ƚ�����ʽ����Ȼ���ٽ���ĸ��ȡֵ���룻�����ʽ��ֵ����ʱ������ĸ��ֵ����Ҫ���ü��ɣ������塱���룮


 ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ����ƽ���ʽ�ֽ���ʽ���У��� ����
��x2+y2����x2-y2����-x2-y2����-x2+y2����-x2+2xy-y2��
A. 1��B��2��C��3��D��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
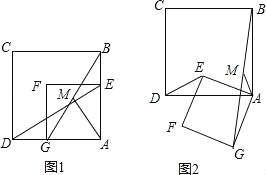
����Ŀ��ͼ1��ͼ2�е�������ABCD���ı���AEFG���������Σ�
��1����ͼ1������DE��BG��MΪ�߶�BG���е㣬����AM��̽��AM��DE��������ϵ��λ�ù�ϵ����֤����Ľ��ۣ�
��2����ͼ1�Ļ����ϣ���������AEFG�Ƶ�A��ʱ�뷽����ת��ͼ2��λ�ã�����DE��BG��MΪ�߶�BG���е㣬����AM��̽��AM��DE��������ϵ��λ�ù�ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��c�������ϵ�λ����ͼ��ʾ������Ӧ�ĵ�ֱ�ΪA��B��C�� ![]()
��1����գ�A��B֮��ľ���Ϊ �� B��C֮��ľ���Ϊ �� A��C֮��ľ���Ϊ��
��2������|a+b|��|c��b|+|b��a|��
��3��a��b��c�������ϵ�λ����ͼ��ʾ����c2=4����b�ĵ�������������a�ľ���ֵ���෴���ǩ�2����a+2b��c��2��a��4c��b����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������롿
��֪����ͼBE��CF����ABC�����ߣ�BE��CF�ཻ��G����֤�� ![]()
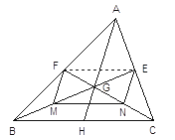
֤��������EF
��E��F�ֱ���AC��AB���е�
��EF��BF��EF��![]() BC
BC
��![]()
��˼�����
��1������AG���ӳ�AG��BC��H����H�Ƿ�ΪBC�е� ����ǡ����ǡ���
��2�������M��N�ֱ���GB��GC���е㣬���ı���EFMN �� �ı��Ρ�
�ڵ�![]() ��ֵΪ ʱ���ı���EFMN �Ǿ��Ρ�
��ֵΪ ʱ���ı���EFMN �Ǿ��Ρ�
�۵�![]() ��ֵΪ ʱ���ı���EFMN �����Ρ�
��ֵΪ ʱ���ı���EFMN �����Ρ�
�����AB��AC����AB��10��BC��16�����ı���EFMN�����![]() ��_________
��_________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ɱ߳�Ϊ1cm�����ɸ������ε����гɵ�ͼ�Σ����е�һ��ͼ����1����������ɣ��ܳ�Ϊ4cm���ڶ���ͼ����4����������ɣ��ܳ�Ϊ10cm��������ͼ����9����������ɣ��ܳ�Ϊ16cm�����ι��ɡ� 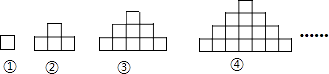
��1�����ĸ�ͼ��������������ɣ��ܳ�Ϊcm��
��2����n��ͼ��������������ɣ��ܳ�Ϊcm��
��3����ijͼ�ε��ܳ�Ϊ58cm�������ͼ���ɶ��ٸ������ε����γɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
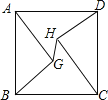
����Ŀ����ͼ������ABCD�߳�Ϊ10��AG=CH=8��BG=DH=6������GH�����߶�GH�ij�Ϊ��������
A. ![]() B.
B. ![]() C.
C. ![]() D. 10-5
D. 10-5![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC������BAC=90������ABC=��ACB���֡�BDC=��BCD���ҡ�1=��2�����3�Ķ�����

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com