
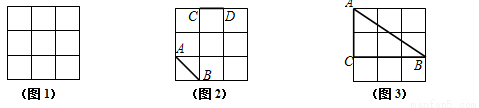
(本小题满分8分)如图,正方形网格中的每个小正方形边长都是1.
(利用网格线进行画图,别忘了标上字母噢!)
(1)在图1中,画一个顶点为格点、面积为5的正方形;
(2)在图2中,已知线段AB、CD,画线段EF,使它与AB、CD组成轴对称图形;
(要求画出所有符合题意的线段)
(3)在图3中,找一格点D,满足:①到CB、CA的距离相等;②到点A、C的距离相等.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014-2015学年山东省滨州市八年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,已知△ABC,O是△ABC内的一点,连接OB、OC,将∠ABO、∠ACO分别记为∠1、∠2,则∠1、∠2、∠A、∠O四个角之间的数量关系是( )
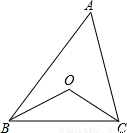
A.∠1+∠0=∠A+∠2 B.∠1+∠2+∠A+∠O=180°
C.∠1+∠2+∠A+∠O=360° D.∠1+∠2+∠A=∠O
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市盐都区八年级上学期期末考试数学试卷(解析版) 题型:解答题
(本题满分10分)小聪和小明沿同一条路同时从学校出发到市图书馆查阅资料,小聪骑电动车,小明骑自行车,当小聪从原路回到学校时,小明刚好到市图书馆,图中折线O﹣A﹣B﹣C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(小时)之间的函数关系,请根据图象回答下列问题:
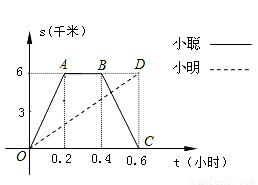
(1)学校到市图书馆的路程是 千米,小聪在市图书馆查阅资料的时间为 小时;
(2)小明骑自行车的速度是 千米/小时;
(3)请你求出小聪返回学校过程中,路程s(千米)与所经过的时间t(小时)之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市盐都区八年级上学期期末考试数学试卷(解析版) 题型:选择题
一次函数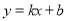 经过第一、二、四象限,则下列正确的是( )
经过第一、二、四象限,则下列正确的是( )
A.k>0,b>0 B.k>0,b<0
C.k<0,b>0 D.k<0,b<0
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市八年级上学期期末考试数学试卷(解析版) 题型:解答题
(本题满分9分)已知:如图1,△ABC中,AB=13,BC=14,AC=15.将线段AB沿过点A的直线翻折,使得点B的对应点E恰好落在BC边上,折痕与BC边相交于点D,如图2所示.
(1)求线段DE的长;

(2)在图2中,若点P为线段AC上一点,且△AEP为等腰三角形,求AP的长.
小李在解决第(2)小题时的过程如下:
① 当EA=EP时,显然不存在;当AE=AP时,则AP=__________;(需填空)
② 对于“当PA=PE时的情形”,小李在解决时遇到了困难.小明老师对小李说:对于这个“直线形”图形直接解决困难时,我们可以建立平面直角坐标系,用一次函数的知识解决.如以点D为坐标原点,BC所在直线为x轴,然后求出AE中垂线的直线解析式,然后求出点P的坐标,最后用勾股定理求出AP的长……
请根据小明老师的提示完成第(2)题中②的求解,你也可以用自己的方法求出AP的长.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市八年级上学期期末考试数学试卷(解析版) 题型:选择题
在如图正方形网格中,每个小正方形的边长都是1,A、B两点在格点上,格点△ABC的面积为1,则格点C的个数为 ( )
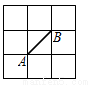
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省株洲市攸县七年级上学期期末测试数学试卷(解析版) 题型:填空题
在长为48cm的线段AB上,取一点D,使AD=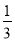 AB ,C为AB的中点,则CD=______________cm.
AB ,C为AB的中点,则CD=______________cm.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滨州市九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,在正方形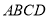 中,
中,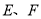 分别是边
分别是边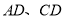 上的点,
上的点,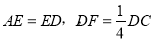 连结
连结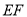 并延长交
并延长交 的延长线于点
的延长线于点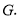

(1)求证: ;
;
(2)若正方形ABCD的边长为8,求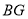 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com