练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．如图，四边形ABCD是矩形，原点O是矩形的中心，AD边平行与x轴，则下列叙述正确的个数是（　　）
    ①A、D两点纵坐标相同，横坐标相反
    ②A、B两点横坐标相同，纵坐标相反．
    ③A、C两点纵横坐标都相反．
    A．1B．2C．3D．0

    分析 直接利用矩形的性质结合点的坐标性质得出各点坐标关系即可．

    解答 解：∵四边形ABCD是矩形，原点O是矩形的中心，AD边平行与x轴，
    ∴①A、D两点纵坐标相同，横坐标相反，正确；
    ②A、B两点横坐标相同，纵坐标相反，正确；
    ③A、C两点纵横坐标都相反，正确．
    故选：C．

    点评 此题主要考查了矩形的性质以及坐标与图形的性质，正确掌握矩形的性质是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    13．如图，已知Rt△ABC中，∠ABC=90°，先把△ABC绕点B顺时针旋转90°至△DBE后，再把△ABC沿射线平移至△FEG，DE、FG相交于点H．
    （1）判断线段DE、FG的位置关系，并说明理由；
    （2）连结CG，求证：四边形CBEG是正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．已知直线y=kx-5经过点M（2，1），那么k=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．如图，长方形ABCD中，AB=5cm，AD=9cm，现将该长方形沿BC方向平移，得到长方形A1B1C1D1，若重叠部分A1B1CD的面积为20cm2，则长方形ABCD向右平移的距离为5cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．已知方程组$\left\{\begin{array}{l}{ax+5y=15（1）}\\{4x-by=-2（2）}\end{array}\right.$，由于甲看错了方程（1）中的 a 得到方程组的解为$\left\{\begin{array}{l}{x=-3}\\{y=1}\end{array}\right.$，乙看错了方程（2）中的 b 得到方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$．若按正确的 a、b 计算，求原方程组的解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

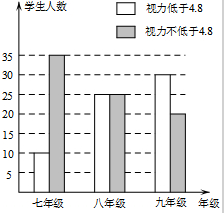    8．在学习了“普查与抽样调查”之后，某校八（1）班数学兴趣小组对该校学生的视力情况进行了抽样调查，并画出了如图所示的条形统计图．请根据图中信息解决下列问题：
    （1）本次抽查活动中共抽查了145名学生；
    （2）已知该校七年级、八年级、九年级学生数分别为360人、400人、540人．
    ①试估算：该校九年级视力不低于4.8的学生约有216名；
    ②请你帮忙估算出该校视力低于4.8的学生数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．如图，在△ABC中，AB=AC，∠BAC=108°，AD、AE将∠BAC三等分交边BC于点D，点E，则下列结论中错误的是（　　）
    A．$\frac{BD}{DE}$=$\frac{\sqrt{5}-1}{2}$B．点D是线段BC的黄金分割点
    C．点E是线段BC的黄金分割点D．点E是线段CD的黄金分割点

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．如图，在菱形ABCD中，DE⊥AB，cosA=$\frac{3}{5}$，BE=2，则BD的值（　　）
    A．2B．$\sqrt{5}$C．$2\sqrt{5}$D．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．如图，在菱形ABCD中，∠ABC=120°，点E是边AB的中点，P是对角线AC上的一个动点，若AB=2，则PB+PE的最小值是（　　）
    A．1B．$\sqrt{3}$C．2D．$2\sqrt{3}$

    查看答案和解析>>

    同步练习册答案