
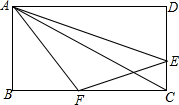
 如图,在矩形ABCD中,AB=3cm,AD=6cm,点E从点C开始沿边CD以1cm/s的速度向点D移动,点F从点B开始沿边BC以2cm/s的速度向点C移动,如果EF同时出发,用t(s)表示移动的时间(0≤t≤3).当t为何值时,以A,B,F为顶点的三角形与以E,F,C为顶点的三角形相似?
如图,在矩形ABCD中,AB=3cm,AD=6cm,点E从点C开始沿边CD以1cm/s的速度向点D移动,点F从点B开始沿边BC以2cm/s的速度向点C移动,如果EF同时出发,用t(s)表示移动的时间(0≤t≤3).当t为何值时,以A,B,F为顶点的三角形与以E,F,C为顶点的三角形相似? 分析 分类讨论:△ABF△∽△ECF,△ABF∽△FCE,根据比例的性质,可得关于t的方程,根据解方程,可得答案.
解答 解:由题意,得BF=2t,EC=t,FC=6-2t,
当△ABF△∽△ECF时,$\frac{AB}{EC}$=$\frac{BF}{FC}$,即$\frac{3}{t}$=$\frac{2t}{6-2t}$,解得t=$\frac{3\sqrt{5}-3}{2}$,t=$\frac{-3\sqrt{5}-3}{2}$(不符合题意要舍去),
当△ABF∽△FCE时,$\frac{AB}{FC}$=$\frac{BF}{CE}$,即$\frac{3}{6-2t}$=$\frac{2t}{t}$,解得t=$\frac{9}{4}$,
当t=$\frac{9}{4}$,t=$\frac{3\sqrt{5}-3}{2}$时,以A,B,F为顶点的三角形与以E,F,C为顶点的三角形相似.
点评 本题考查了相似三角形,利用相似三角形的性质的出关于t的方程是解题关键,要分类讨论,以防遗漏.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点P是菱形ABCD的对角线DB的延长线上一点,连接PC并延长,交AD的延长线于E,AB的延长线交PC于点F.
如图,点P是菱形ABCD的对角线DB的延长线上一点,连接PC并延长,交AD的延长线于E,AB的延长线交PC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com