
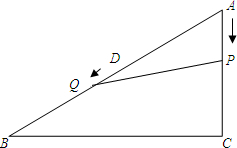
 在Rt△ABC中,AC=6cm,BC=8cm,点P由点A出发,沿AC方向运动,速度为2cm/s;同时点Q由AB中点D出发,沿DB向B运动,速度为1cm/s;连接PQ,若设运动时间为t(s) (0<t≤3).
在Rt△ABC中,AC=6cm,BC=8cm,点P由点A出发,沿AC方向运动,速度为2cm/s;同时点Q由AB中点D出发,沿DB向B运动,速度为1cm/s;连接PQ,若设运动时间为t(s) (0<t≤3).分析 (1)过Q做QM⊥AC于M,在Rt△ABC中,由勾股定理得:AB=10cm,根据三角形相似即可得到答案;
(2))由△APQ的面积与四边形BCPQ的面积比是7:8,得到S△APQ:S△ABC=7:15,列方程$\frac{4}{5}$t2+4t=$\frac{7}{15}$×$\frac{1}{2}×6×8$,求得t=2;
(3)当点D在PQ的垂直平分线上时,PD=QD,过点D作DN⊥AC于N,列方程得到方程无解,所以不存在某一时刻t,使点D在PQ的垂直平分线上.
解答  解:(1)过Q做QM⊥AC于M,如图1,
解:(1)过Q做QM⊥AC于M,如图1,
∵Rt△ABC中,
AC=6cm,BC=8cm,
由勾股定理得:AB=10cm,
∵点P由点A出发,沿AC方向运动,速度为2cm/s;同时点Q由AB中点D出发,沿DB向B运动,速度为1cm/s,
∴AC=2t,AQ=5+t,
∵QM⊥AC,BC⊥AC,
∴QM∥BC,
∴△AQM∽△ABC,
∴$\frac{QM}{BC}=\frac{AQ}{AB}$,
即$\frac{QM}{8}=\frac{5+t}{10}$,
解得:QM=4+$\frac{4}{5}t$,
∴y=$\frac{1}{2}$AP•QM=$\frac{1}{2}$×2t(4+$\frac{4}{5}$t),
即y=$\frac{4}{5}$t2+4t;
(2)存在,
∵△APQ的面积与四边形BCPQ的面积比是7:8,
∴S△APQ:S△ABC=7:15,
∴$\frac{4}{5}$t2+4t=$\frac{7}{15}$×$\frac{1}{2}×6×8$,
解得:t=2,(负值舍去),
∴当t=2时,△APQ的面积与四边形BCPQ的面积比是7:8;
(3)如图2,当点D在PQ的垂直平分线上时,PD=QD,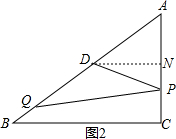
过点D作DN⊥AC于N,
则DN=$\frac{1}{2}$BC=4,PN=2t-3,
∴PD=$\sqrt{{4}^{2}{+(2t-3)}^{2}}$,
∴t=$\sqrt{{4}^{2}{+(2t-3)}^{2}}$,
化整式方程为:3t2-12t+25=0,
∵△=122-4×3×5<0,
∴方程无解,
∴不存在某一时刻t,使点D在PQ的垂直平分线上.
点评 本题考查了动点问题,相似三角形的判定和性质,勾股定理,一元二次解的情况,正确的画出图形是解题的关键.


科目:初中数学 来源: 题型:解答题
 在矩形ABCD中,点E,点F为对角线BD上两点,DE=EF=FB.
在矩形ABCD中,点E,点F为对角线BD上两点,DE=EF=FB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,梯形OABC中,CB∥OA,O为坐标原点,B(2,4),C(0,4),tan∠BAO=2,动点Q 从点O出发,以每秒1个单位的速度沿线段OA运动,到点A停止,过点Q作OP⊥x轴交折线C-B-A于点P,以PQ为一边向左作正方形PQRS,设运动时间为t (秒),正方形PQRS与梯形OABC重叠的面积为S(平方单位).
如图,梯形OABC中,CB∥OA,O为坐标原点,B(2,4),C(0,4),tan∠BAO=2,动点Q 从点O出发,以每秒1个单位的速度沿线段OA运动,到点A停止,过点Q作OP⊥x轴交折线C-B-A于点P,以PQ为一边向左作正方形PQRS,设运动时间为t (秒),正方形PQRS与梯形OABC重叠的面积为S(平方单位).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
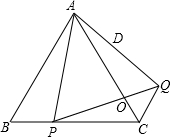 如图,已知等边△ABC的边长为a,点P是BC边上一动点,以AP为边作等边△APQ,边PQ交AC于点O,连接CQ,
如图,已知等边△ABC的边长为a,点P是BC边上一动点,以AP为边作等边△APQ,边PQ交AC于点O,连接CQ,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
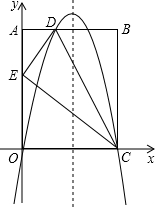 如图,在平面直角坐标系中,已知矩形OABC的三个顶点A(0,10),B(8,10),C(8,0),过O、C两点的抛物线y=ax2+bx+c与线段AB交于点D,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.
如图,在平面直角坐标系中,已知矩形OABC的三个顶点A(0,10),B(8,10),C(8,0),过O、C两点的抛物线y=ax2+bx+c与线段AB交于点D,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
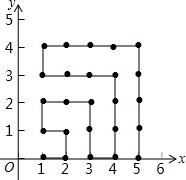 如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)根据这个规律,第2014个点的坐标为(45,11).
如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)根据这个规律,第2014个点的坐标为(45,11).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com