解:(1)由“上加下减”的原则可知,把一次函数y=-x的图象向上平移1个单位后得到一个新的函数的图象的解析式为y=-x+1;
由“左加右减”的原则可知,把一次函数y=-x+1的图象向右平移3个单位后的图象的解析式为y=-(x-3)+1,即y=-x+4.
故答案为:y=-x+1,y=-x+4;
(2)由“上加下减”的原则可知,把反比例函数y=

的图象向上平移2个单位后得到一个新的函数的图象的解析式为y=

+2;
由“左加右减”的原则可知,把一反比例函数y=

+2的图象向右平移2个单位后的图象的解析式为y=

+2.
故答案为:y=

+2,y=

+2;
(3)∵函数

可化为y=-

+2的形式,
∴把函数y=-

先向左平移1个单位,再向上平移2个单位即可得到函数y=
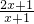
的图象;
(4)设新函数的解析式是y=

+b,
∵令x=0,则y=-

+b,令y=0,则x=

,
∴函数图象与坐标轴的两交点为(0,-

+b)、(

,0),
∵新函数的图象与坐标轴的两个交点与原点构成一个等腰三角形
∴-

+b=±

,解得b=2,-2,

,
当b=

时函数图象与坐标轴的交点只有一个是原点,故舍去,
∴b的值为±2,
∴新函数的解析式为:y=

+2或y=

-2.
分析:(1)直接根据函数图象平移的法则进行解答即可;
(2)直接根据函数图象平移的法则进行解答即可;
(3)先把函数

化为y=-

+2的形式,再根据函数图象平移的法则进行解答即可;
(4)设新函数的解析式为y=

+b,再由坐标轴上点的坐标特点得出函数图象与两坐标轴的交点,由等腰三角形的性质即可求出b的值.
点评:本题考查的是反比例函数综合题,熟知“上加下减,左加右减”的法则是解答此题的关键.

 的图象向上平移2个单位得反比例函数______的图象,若再向右平移2个单位后可以得到反比例函数______的图象;
的图象向上平移2个单位得反比例函数______的图象,若再向右平移2个单位后可以得到反比例函数______的图象; 的图象可以由函数
的图象可以由函数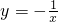 图象如何平移得到的;
图象如何平移得到的; 的图象将此函数向右平移2个单位后,再进行上下平移,使新函数的图象与坐标轴的两个交点与原点构成一个等腰三角形,求新函数的解析式.
的图象将此函数向右平移2个单位后,再进行上下平移,使新函数的图象与坐标轴的两个交点与原点构成一个等腰三角形,求新函数的解析式. 的图象向上平移2个单位后得到一个新的函数的图象的解析式为y=
的图象向上平移2个单位后得到一个新的函数的图象的解析式为y= +2;
+2; +2的图象向右平移2个单位后的图象的解析式为y=
+2的图象向右平移2个单位后的图象的解析式为y= +2.
+2. +2,y=
+2,y= +2;
+2; 可化为y=-
可化为y=- +2的形式,
+2的形式, 先向左平移1个单位,再向上平移2个单位即可得到函数y=
先向左平移1个单位,再向上平移2个单位即可得到函数y=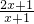 的图象;
的图象; +b,
+b, +b,令y=0,则x=
+b,令y=0,则x= ,
, +b)、(
+b)、( ,0),
,0), +b=±
+b=± ,解得b=2,-2,
,解得b=2,-2, ,
, 时函数图象与坐标轴的交点只有一个是原点,故舍去,
时函数图象与坐标轴的交点只有一个是原点,故舍去, +2或y=
+2或y= -2.
-2. 化为y=-
化为y=- +2的形式,再根据函数图象平移的法则进行解答即可;
+2的形式,再根据函数图象平移的法则进行解答即可; +b,再由坐标轴上点的坐标特点得出函数图象与两坐标轴的交点,由等腰三角形的性质即可求出b的值.
+b,再由坐标轴上点的坐标特点得出函数图象与两坐标轴的交点,由等腰三角形的性质即可求出b的值.


 的图象向上平移2个单位得反比例函数______的图象,若再向右平移2个单位后可以得到反比例函数______的图象;
的图象向上平移2个单位得反比例函数______的图象,若再向右平移2个单位后可以得到反比例函数______的图象; 的图象可以由函数
的图象可以由函数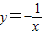 图象如何平移得到的;
图象如何平移得到的; 的图象将此函数向右平移2个单位后,再进行上下平移,使新函数的图象与坐标轴的两个交点与原点构成一个等腰三角形,求新函数的解析式.
的图象将此函数向右平移2个单位后,再进行上下平移,使新函数的图象与坐标轴的两个交点与原点构成一个等腰三角形,求新函数的解析式.