练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．计算：47°30′-14°12′50″=33°17′10″．

    分析 根据度分秒的和减法，可得答案．

    解答 解：47°30′-14°12′50″=33°17′10″，
    故答案为：33°17′10″．

    点评 本题考查了度分秒的换算，利用度分秒的减法是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    6．已知?ABCD的面积为4，对角线AC在y轴上，点D在第一象限内，且AD∥x轴，当双曲线y=$\frac{k}{x}$经过B、D两点时，则k=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

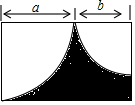    7．如图所示，用含a、b字母的代数式表示图中阴影部分的面积为${a}^{2}+ab-\frac{π{a}^{2}}{4}-\frac{π{b}^{2}}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．如图，直线AB、CD相交于点O，OE平分∠AOC，∠BOC-∠BOD=30°，则∠COE的度数是37.5°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．已知两个相似的三角形的面积之比是16：9，那么这两个三角形的周长之比是4：3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．把下列各式的分母有理化．
    $\frac{\sqrt{10}}{\sqrt{5}}$=$\sqrt{2}$；$\frac{\sqrt{6}}{\sqrt{24}}$=$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

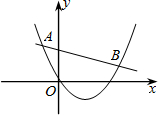    8．已知二次函数y1=ax2+bx+c（a≠0）与一次函数y2=kx+m（k≠0）的图象交于点A（-2，4），B（5，1），如图所示，则能使y1＞y2成立的x的取值范围是x＜-2或x＞5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．用直接开平方法解方程．
    （1）x2-$\frac{36}{25}$=0
    （2）3x2-9=0
    （3）（x-2）2=5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．某港口位于东西方向的海岸线上．“远航”号、“海天”号轮船同时离开港口，各自沿一固定方向航行，“远航”号每小时航行16海里，“海天”号每小时航行12海里．它们离开港口一个半小时后相距30海里．
    （1）求PQ、PR的长．
    （2）如果知道“远航”号沿东北方向航行，能知道“海天”号沿哪个方向航行？为什么？

    查看答案和解析>>

    同步练习册答案