
分析 (1)根据题中的计算填写答案即可;
(2)按照题中所给的计算方法,求解即可;
(3)根据题中所给的计算方法,进行求解判断即可.
解答 解:(1)∵($\frac{2}{3}$)2=$\frac{2}{3}$×$\frac{2}{3}$,($\frac{3}{2}$)-2=$\frac{1}{(\frac{3}{2})^{2}}$=$\frac{1}{\frac{3}{2}}×\frac{1}{\frac{3}{2}}$=$\frac{2}{3}×\frac{2}{3}$,
∴($\frac{2}{3}$)2=($\frac{3}{2}$)-2.
(2)($\frac{5}{4}$)3=$\frac{5}{4}×\frac{5}{4}$×$\frac{5}{4}$,($\frac{4}{5}$)-3=$\frac{1}{(\frac{4}{5})^{3}}$=$\frac{1}{\frac{4}{5}}×\frac{1}{\frac{4}{5}}$×$\frac{1}{\frac{4}{5}}$=$\frac{5}{4}×\frac{5}{4}$×$\frac{5}{4}$.
故($\frac{5}{4}$)3=($\frac{4}{5}$)-3.
(3)($\frac{b}{a}$)-m=($\frac{a}{b}$)m (ab≠0).
点评 本题考查了负整数指数幂,解答本题的关键在于按照题中所给的方法来进行计算并得出各个数之间的关系.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD中,对角线AC、BD相交于点O,O为AC、BD的中点,AB=10,AC=16,BD=12.
如图,四边形ABCD中,对角线AC、BD相交于点O,O为AC、BD的中点,AB=10,AC=16,BD=12.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)指出图中有1个边长为a的正方形;有4个边长为b的正方形有4个两边长分别为a和b的矩形
(1)指出图中有1个边长为a的正方形;有4个边长为b的正方形有4个两边长分别为a和b的矩形查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
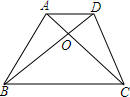 如图,梯形ABCD中,AD∥BC,△AOB的面积是16平方厘米,△AOD的面积是12平方厘米,求:(1)△BOC和△COD面积;(2)$\frac{AO}{AC}$的值.
如图,梯形ABCD中,AD∥BC,△AOB的面积是16平方厘米,△AOD的面积是12平方厘米,求:(1)△BOC和△COD面积;(2)$\frac{AO}{AC}$的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com