我们假设把两边平方和等于第三边平方的两倍的三角形叫做奇异三角形.如果Rt△ABC是奇异三角形,在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,其中,a=1,那么b= .
【答案】
分析:由三角形ABC为直角三角形,利用勾股定理列出关系式c
2=a
2+b
2,记作①,再由新定义两边平方和等于第三边平方的2倍的三角形叫做奇异三角形,列出关系式2a
2=b
2+c
2,记作②,或2b
2=a
2+c
2,记作③,由以上关系式即可求出b的值.
解答:解:∵Rt△ABC中,∠ACB=90°,AB=c,AC=b,BC=a,
∴根据勾股定理得:c
2=a
2+b
2,记作①,
又∵Rt△ABC是奇异三角形,
∴2a
2=b
2+c
2,②
将①代入②得:a
2=2b
2,即a=
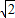
b(不合题意,舍去),
∴2b
2=a
2+c
2,③
将①代入③得:b
2=2a
2,即b=
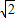
a,
∴a=1时,那么b=
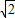
,
故答案为:
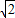
.
点评:此题考查了勾股定理,以及新定义,弄清题中的新定义,熟练掌握勾股定理是解本题的关键.

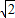 b(不合题意,舍去),
b(不合题意,舍去),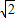 a,
a,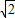 ,
,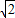 .
.
