
分析 首先把a2+b+1+|$\sqrt{c-1}$-2|=10a+2$\sqrt{b-4}$-21,化为a2-10a+25+b-4-2$\sqrt{b-4}$+1+|$\sqrt{c-1}$-2|=(a-5)2+($\sqrt{b-4}$-1)2+|$\sqrt{c-1}$-2|=0,然后利用非负数的性质确定三边的值,进一步判断即可.
解答 解:∵a2+b+1+|$\sqrt{c-1}$-2|=10a+2$\sqrt{b-4}$-21,
∴a2-10a+25+b-4-2$\sqrt{b-4}$+1+|$\sqrt{c-1}$-2|=(a-5)2+($\sqrt{b-4}$-1)2+|$\sqrt{c-1}$-2|=0,
∴a-5=0,$\sqrt{b-4}$-1=0,|$\sqrt{c-1}$-2|=0,
解得:a=5,b=5,c=5,
∴△ABC为等边三角形.
点评 此题考查配方法的运用,非负数的性质,掌握完全平方公式和二次根式的意义是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
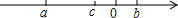 已知有理数a,b,c在数轴上的位置如图所示:化简$\frac{|abc|}{abc}+\frac{a+b+c}{|a+b+c|}-\frac{|bc|}{bc}-\frac{c-b}{|c-b|}-\frac{a}{|a|}$.
已知有理数a,b,c在数轴上的位置如图所示:化简$\frac{|abc|}{abc}+\frac{a+b+c}{|a+b+c|}-\frac{|bc|}{bc}-\frac{c-b}{|c-b|}-\frac{a}{|a|}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com