
【题目】如图,在平面直角坐标系中,一次函数y=![]() x﹣2的图象分别交x、y轴于点A、B,抛物线y=x2+bx+c经过点A、B,点P为第四象限内抛物线上的一个动点.
x﹣2的图象分别交x、y轴于点A、B,抛物线y=x2+bx+c经过点A、B,点P为第四象限内抛物线上的一个动点.
(1)求此抛物线的函数解析式;
(2)过点P作PM∥y轴,分别交直线AB、x轴于点C、D,若以点P、B、C为顶点的三角形与以点A、C、D为顶点的三角形相似,求点P的坐标;
(3)当∠PBA=2∠OAB时,求点P的坐标.

【答案】(1) ;(2)点P的坐标是(
;(2)点P的坐标是(![]() ,﹣5)或(
,﹣5)或(![]() ,﹣2);(3)点P的坐标是(3,
,﹣2);(3)点P的坐标是(3,![]() ).
).
【解析】
(1)本题所求二次函数的解析式含有两个待定字母,一般需要两个点的坐标建立方程组,现在可求A、B点坐标,代入列方程组可解答;
(2)根据∠ADC=90°,∠ACD=∠BCP,可知相似存在两种情况:
①当∠CBP=90°时,如图1,过P作PN⊥y轴于N,证明△AOB∽△BNP,列比例式可得结论;②当∠CPB=90°时,如图2,则B和P是对称点,可得P的纵坐标为﹣2,代入抛物线的解析式可得结论;
(3)设点A关于y轴的对称点为A′,求出直线A′B的解析式,再联立抛物线的解析式解答即可.
解:(1)令x=0,得y=![]() x﹣2=-2,则B(0,﹣2),
x﹣2=-2,则B(0,﹣2),
令y=0,得![]() x﹣2=0,解得x=4,
x﹣2=0,解得x=4,
则A(4,0),
把A(4,0),B(0,﹣2)代入y=x2+bx+c(a≠0)中,
得![]() 解得
解得 .
.
∴抛物线的解析式为: .
.
(2)∵PM∥y轴,
∴∠ADC=90°.
∵∠ACD=∠BCP,
∴以点P、B、C为顶点的三角形与以点A、C、D为顶点的三角形相似,存在两种情况:
①当∠CBP=90°时,如图,过P作PN⊥y轴于N,
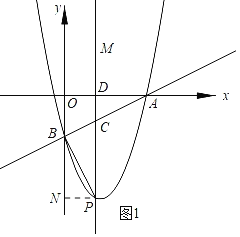
∵∠ABO+∠PBN=∠ABO+∠OAB=90°,
∴∠PBN=∠OAB,
∵∠AOB=∠BNP=90°,
∴Rt△PBN∽Rt△BAO.
∴![]() =
=![]() .
.
设P(x,x2-![]() x-2).
x-2).
∴![]() =
=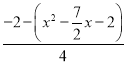 ,化简,得x2-
,化简,得x2-![]() x=0.
x=0.
解得x=0(舍去)或x=![]() .
.
当x=![]() 时,y=x2-
时,y=x2-![]() x-2=-5..
x-2=-5..
∴p(![]() ,﹣5);
,﹣5);
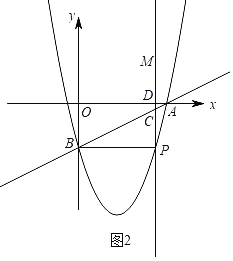
②当∠CPB=90°时,如图2,则PB∥x轴,所以B和P是对称点.
所以当y=﹣2时,即x2-![]() x-2=-2,解得x=0(舍去)或x=
x-2=-2,解得x=0(舍去)或x=![]() .
.
∴P(![]() ,﹣2).
,﹣2).
综上,点P的坐标是(![]() ,﹣5)或(
,﹣5)或(![]() ,﹣2).
,﹣2).
(3)设点A关于y轴的对称点为A′,则A′B=AB.
∴∠BAO=∠B′AO.
直线A′B交抛物线于P.
∴∠PBA=∠BAO+∠BA′O=2∠BAO.
∵A(4,0),
∴A′(﹣4,0).
设直线A′B的解析式为y=kx+b(k≠0).
∵B(0,﹣2).
∴![]()
解得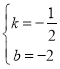
∴直线A′B的解析式为y=![]() x-2.
x-2.
由方程组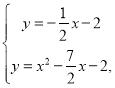 得x2﹣3x=0.
得x2﹣3x=0.
解得x=0(舍去)或x=3.
当x=3时,y=![]() x-2=-
x-2=-![]() .
.
所以点P的坐标是(3,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,对角线
中,对角线![]() 相交于点
相交于点![]() ,以
,以![]() 为边向外作等边
为边向外作等边![]() ,连接
,连接![]() 交
交![]() 于
于![]() 若点
若点![]() 为
为![]() 的延长线上一点,连接
的延长线上一点,连接![]() ,连接
,连接![]() 且
且![]() 平分
平分![]() ,下列选项正确的有( )
,下列选项正确的有( )
①![]() ;②
;②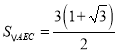 ;③
;③![]() ;④
;④![]()

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情在全球蔓延,造成了严重的人员伤亡和经济损失,其中一个原因是新冠肺炎病毒传播速度非常快.一个人如果感染某种病毒,经过了两轮的传播后被感染的总人数将达到64人.
(1)求这种病毒每轮传播中一个人平均感染多少人?
(2)按照上面的传播速度,如果传播得不到控制,经过三轮传播后一共有多少人被感染?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(列方程解应用题)为提高学生的阅读兴趣,某学校建立了共享书架,并购买了一批书籍.其中购买A种图书花费了3000元,购买B种图书花费了1600元,A种图书的单价是B种图书的1.5倍,购买A种图书的数量比B种图书多20本,求A和B两种图书的单价分别为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
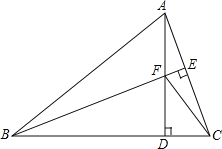
【题目】如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,CD=![]() ,AD与BE交于点F,连接CF,则AD的长为_____.
,AD与BE交于点F,连接CF,则AD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
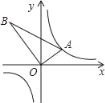
【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=![]() 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y=![]() 的图象上,则k的值为_____.
的图象上,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图,其中每个小正方形的边长为1个单位长度.
(1)画出△ABC关于原点O的中心对称图形△A1B1C1;
(2)画出将△ABC绕点C顺时针旋转90°得到△A2B2C2.
(3)在(2)的条件下,求点A旋转到点A2所经过的路线长(结果保留π).
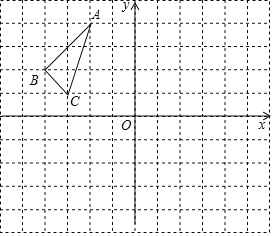
查看答案和解析>>
科目:初中数学 来源: 题型:
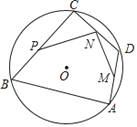
【题目】如图,AB,BC是⊙O的弦,∠B=60°,点O在∠B内,点D为![]() 上的动点,点M,N,P分别是AD,DC,CB的中点.若⊙O的半径为2,则PN+MN的长度的最大值是( )
上的动点,点M,N,P分别是AD,DC,CB的中点.若⊙O的半径为2,则PN+MN的长度的最大值是( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com