
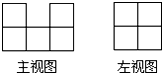
 如图,是由若干个完全相同的小正方体组成的一个几何体的主视图和左视图,则组成这个几何体的小正方体的个数是5或6或7或8或9或10.
如图,是由若干个完全相同的小正方体组成的一个几何体的主视图和左视图,则组成这个几何体的小正方体的个数是5或6或7或8或9或10.  培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,⊙O是等边三角形ABC的外接圆,⊙O的半径为2,则等边△ABC的边长为( )
如图,⊙O是等边三角形ABC的外接圆,⊙O的半径为2,则等边△ABC的边长为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 △ABC在网络中的位置如图所示,则cos∠ACB的值为( )
△ABC在网络中的位置如图所示,则cos∠ACB的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若连接四边形中点所形成的四边形是矩形,则原四边形一定是菱形 | |
| B. | 若连接四边形中点所形成的四边形是菱形,则原四边形一定是矩形 | |
| C. | 若连接四边形中点所形成的四边形是正方形,则原四边形一定是正方形 | |
| D. | 以上说法均不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com