
分析 根据多边形的内角和公式(n-2)•180°可知,多边形的内角和是180°的倍数,然后求出多边形的边数以及多加的外角的度数即可得解.
解答 解:设多边形的边数为n,多加的外角度数为α,则
(n-2)•180°=1665°-α,
∵1665°=9×180°+45°,内角和应是180°的倍数,
∴同学多加的一个外角为45°,
∴这是9+2=11边形的内角和,
这个多边形一定有一个内角是180°-45°=135°.
答:他计算的是11边形的内角和,这个多边形一定有一个内角是135°.
点评 本题考查了多边形的内角和公式,根据多边形的内角和公式判断出多边形的内角和公式是180°的倍数是解题的关键.


科目:初中数学 来源: 题型:解答题
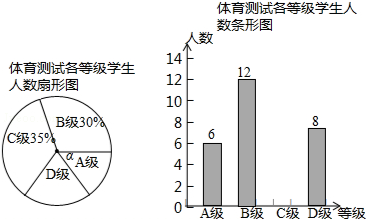
 今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某数学兴趣小组在本校学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查结果,绘制了如图的统计图,结合统计图,回答下列问题.
今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某数学兴趣小组在本校学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查结果,绘制了如图的统计图,结合统计图,回答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
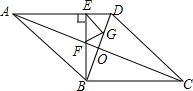 菱形ABCD中,对角线AC,BD交于点O,BE⊥AD交AC于F,AF=BD,G为BD上的点,EG∥AB.
菱形ABCD中,对角线AC,BD交于点O,BE⊥AD交AC于F,AF=BD,G为BD上的点,EG∥AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
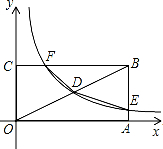 如图,矩形OABC的顶点A、C分别在x、y的正半轴上,点D为对角线OB的中点,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点D,且与AB、BC分别交于E、F两点,若四边形BEDF的面积为4.5,则k的值为( )
如图,矩形OABC的顶点A、C分别在x、y的正半轴上,点D为对角线OB的中点,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点D,且与AB、BC分别交于E、F两点,若四边形BEDF的面积为4.5,则k的值为( )| A. | 2 | B. | 3 | C. | 6 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省南通市七年级3月月考数学试卷(解析版) 题型:解答题
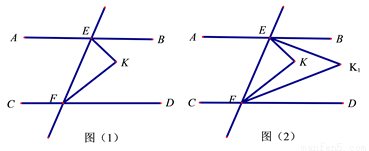
已知:如图(1),直线AB∥CD,EF分别交AB、CD于E、F两点,∠BEF、∠DFE的平分线相交于点K.(1)求∠EKF的度数.(计算过程不准用三角形内角和)(2)如图(2),∠BEK、∠DFK的平分线相交于点K1,问∠K1与∠K的度数是否存在某种特定的等量关系?写出结论并证明.(3)在图2中作∠BEK1、∠DFK1的平分线相交于点K2,作∠BEK2、∠DFK2的平分线相交于点K3,依此类推,作∠BEKn、∠DFKn的平分线相交于点Kn+1,请用含的n式子表示∠Kn+1的度数.(直接写出答案,不必写解答过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com