
分析 (1)待定系数法求解可得;
(2)根据“总利润=单件利润×销售量”列出函数解析式并配方,结合二次函数的性质即可得出函数的最值.
解答 解:(1)设一次函数的解析式为y=kx+b,
依题意有:$\left\{\begin{array}{l}{120k+b=100}\\{130k+b=95}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=160}\end{array}\right.$,
∴y与x的函数关系式为y=-$\frac{1}{2}$x+160,(100≤x≤160);
(2)依题意有:W=(x-80)(-$\frac{1}{2}$x+160)=-$\frac{1}{2}$(x-200)2+7200,
∵a=-$\frac{1}{2}$<0,
∴当x<200时,y随x的增大而增大,
∴当x=160时,W有最大值,最大值为6400元,
答:当销售单价x定为每瓶160元时,销售利润最大,最大利润是6400元.
点评 本题主要考查二次函数的应用,熟练掌握待定系数法求函数解析式,并根据题意确定相等关系列出函数解析式是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 0.10261×1011元 | B. | 10.261×109元 | C. | 1.0261×1010元 | D. | 1.0261×1011元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -$\frac{1}{3}$ | C. | -$\sqrt{2}$ | D. | -$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
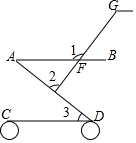 如图所示是婴儿车的平面示意图,其中AB∥CD,∠1=121°,∠3=42°,那么∠2的度数为( )
如图所示是婴儿车的平面示意图,其中AB∥CD,∠1=121°,∠3=42°,那么∠2的度数为( )| A. | 79° | B. | 89° | C. | 59° | D. | 91° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 诗词数量(首) | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 人数 | 3 | 4 | 4 | 5 | 7 | 5 | 1 | 1 |
| A. | 11,7 | B. | 7,5 | C. | 8,8 | D. | 8,7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3-$\sqrt{5}$ | B. | $\sqrt{5}$-3 | C. | -3-$\sqrt{5}$ | D. | 3+$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知?ABCD.
如图,已知?ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com