【题目】如图，点E在△ABC外部，点D在边BC上，DE交AC于点F.若∠1=∠2=∠3，AC=AE,求证△ABC≌△ADE．
【答案】证明过程见解析
【解析】试题分析：要想证明△ABC≌△ADE,全等的条件,∵∠1=∠2=∠3，
∴∠2+∠DAC=∠1+∠DAC，∴∠BAC=∠DAE，又∵∠DFC=∠AFE，∠3=∠1，
∴在△ADE和△ABC中,由三角形的内角和定理得∠3+∠C+∠DFC=∠1+∠E+∠AFE，
∵∠DFC=∠AFE,∴∠C=∠E，又已知AD=AB，∴△ABC≌△ADE（AAS）
试题解析： （1）由三角形的内角和定理△AEF与△DCF中，
∵∠2=∠3，∠AFE=∠CFD， ∴∠C=∠E；∵∠1=∠2， ∠BAC=∠1+∠DAC,
∠DAE=∠2+∠DAC ∴∠BAC=∠DAE 又∵AC=AE， ∴△ABC≌△ADE(ASA)
阅读快车系列答案科目：初中数学 来源： 题型：
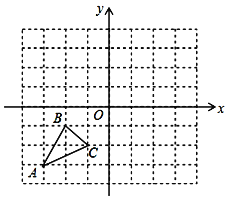
【题目】如图，已知A（-3，-3），B（-2，-1），C（-1.-2）是坐标平面上三点.
（1）写出点C关于y轴的对称点C’的坐标；
（2）画出将△ABC先向上平移5个单位，再向右平移3个单位后所对应的△A1B1C1.并写出△A1B1C1的各顶点坐标；
（3）将点C’向上平移
个单位后，点C’恰好落在△A1B1C1内，请你写出符合条件的一个整数
.（直接写出答案）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（本题满分10分）
有理数x，y在数轴上对应点如图所示：
（1）在数轴上表示－x， 
；
（2）试把x，y，0，－x， 
这五个数从小到大用“＜”号连接；
（3）化简： 
－
+
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】平行四边形一边长为12cm，那么它的两条对角线的长度可以是（ ）
A. 8cm和14cm B. 10cm 和14cm C. 18cm和20cm D. 10cm和34cm
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在△OMN中，∠MON=90°，OM=6cm，∠OMN=30°.等边△ABC的顶点B与点O重合，BC在OM上，点A恰好在MN上.
（1）求等边△ABC的边长；
（2）如图2,将等边△ABC沿OM方向以1cm/s的速度平移,边AB、AC分别与MN交于点E、F,在△ABC平移的同时,点P从△ABC的顶点B出发,以2cm/s的速度沿折线B→A→C运动,当点P达到点C时,点P停止运动,△ABC也随之停止平移．设△ABC平移时间为t（s）
①用含t的代数式表示AE的长,并写出t的取值范围；
②在点P沿折线B→A→C运动的过程中,是否在某一时刻,点P、E、F组成的三角形为等腰三角形?若存在,求出此时t值；若不存在,请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】服装店销售某款服装，一件服装的标价为300元，若按标价的八折销售，仍可获利60元，则这款服装每件的标价比进价多
A. 60元 B. 80元 C. 120元 D. 180元
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】
已知n边形的内角和θ=（n-2）×180°.
（1）甲同学说，θ能取360°；而乙同学说，θ也能取630°.甲、乙的说法对吗？若对，求出边数n.若不对，说明理由；
（2）若n边形变为（n+x）边形，发现内角和增加了360°，用列方程的方法确定x.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某自行车厂一周计划生产1400辆自行车，平均每天生产200辆，由于各种原因实际每天生产量与计划量相比有出入．下面是一周中每天的生产情况记录表（超过200辆记为正、不足200辆记为负）：
（1）、根据记录可知前三天共生产 辆；
（2）、产量最多的一天比产量最少的一天多生产 _________ 辆；
（3）、该厂实行计件工资制，当一周实际生产的自行车总量不超过1400辆时，每辆车60元；当一周实际生产的自行车总量超过1400辆时，其中1400辆车每辆车60元，超过1400辆的部分每辆车75元，那么该厂工人这一周的工资总额是多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com