
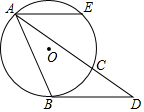
 如图,AB、AC是⊙O的弦,过点B作⊙O的切线交AC的延长线于点D,点E是弧AC的中点,连接AE,若∠EAB=65°,则∠D的度数是( )
如图,AB、AC是⊙O的弦,过点B作⊙O的切线交AC的延长线于点D,点E是弧AC的中点,连接AE,若∠EAB=65°,则∠D的度数是( )| A. | 25° | B. | 50° | C. | 65° | D. | 70° |
分析 连接OB,OE,BE,根据圆周角定理得到∠BOE=130°,根据等腰三角形的性质得到∠OEB=25°,根据垂径定理得到OE⊥CA,由三角形的内角和得到∠EFA=65°,根据弦切角定理得到∠BDE=∠BAE=65°,于是得到结论.
解答 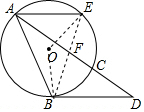 解:连接OB,OE,BE,
解:连接OB,OE,BE,
∵∠EAB=65°,
∴∠BOE=130°,
∵OE=OB,
∴∠OEB=25°,
∵点E是弧AC的中点,
∴OE⊥CA,
∴∠EFA=65°,
∵BD是⊙O的切线,
∴∠BDE=∠BAE=65°,
∵∠DFB=∠EFA=65°,
∴∠D=50°.
故选B.
点评 本题考查了切线的性质,垂径定理,等腰三角形的性质,三角形的内角和,正确的作出辅助线是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y2>y1>y3 | D. | y2>y3>y1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
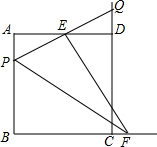 在边长为2的正方形ABCD中,P为AB上的一动点,E为AD中点,PE交CD延长线于Q,过E作EF⊥PQ交BC的延长线于F,则下列结论:①△APE≌△DQE;②PQ=EF;③当P为AB中点时,CF=$\sqrt{2}$;④若H为QC的中点,当P从A移动到B时,线段EH扫过的面积为$\frac{1}{2}$,其中正确的是( )
在边长为2的正方形ABCD中,P为AB上的一动点,E为AD中点,PE交CD延长线于Q,过E作EF⊥PQ交BC的延长线于F,则下列结论:①△APE≌△DQE;②PQ=EF;③当P为AB中点时,CF=$\sqrt{2}$;④若H为QC的中点,当P从A移动到B时,线段EH扫过的面积为$\frac{1}{2}$,其中正确的是( )| A. | ①② | B. | ①②④ | C. | ②③④ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
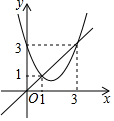 函数y=x2+bx+c与y=x的图象如图所示,则下列结论中正确的是( )
函数y=x2+bx+c与y=x的图象如图所示,则下列结论中正确的是( )| A. | 当1<x<3时,x2+(b-1)x+c<0 | B. | b+c=1 | ||
| C. | 3b+c=6 | D. | b2-4c>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
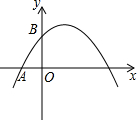 如图,抛物线y=-x2+ax+4与x轴负半轴交于点A,与y轴交于点B,且tan∠ABO=$\frac{1}{4}$,点C(x1,y1),D(x2,y2)是抛物线y=-x2+ax+4上两点,当x1≤x≤x2,y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$.则下列结论正确的是( )
如图,抛物线y=-x2+ax+4与x轴负半轴交于点A,与y轴交于点B,且tan∠ABO=$\frac{1}{4}$,点C(x1,y1),D(x2,y2)是抛物线y=-x2+ax+4上两点,当x1≤x≤x2,y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$.则下列结论正确的是( )| A. | a=-3 | B. | y2<4 | C. | |x1-x2|=1 | D. | |x1-$\frac{3}{2}$|>|x2-$\frac{3}{2}$| |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 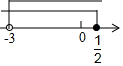 | B. |  | C. | 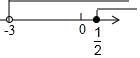 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
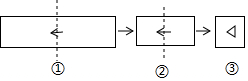 把一张长方形纸片按如图①、图②的方式从右向左连续对折两次后得到图③,再在图③中挖去一个如图所示的三角形小孔,则重新展开后得到的图形是( )
把一张长方形纸片按如图①、图②的方式从右向左连续对折两次后得到图③,再在图③中挖去一个如图所示的三角形小孔,则重新展开后得到的图形是( )| A. | 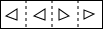 | B. | 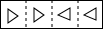 | C. | 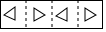 | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com