
【题目】如图,在菱形ABCD中,对角线AC与BD相交于点O,MN过点O且与边AD、BC分别交于点M和点N.
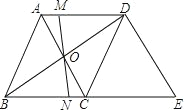
(1)请你判断OM与ON的数量关系,并说明理由;
(2)过点D作DE∥AC交BC的延长线于E,当AB=5,AC=6时,求△BDE的周长.
【答案】(1) OM=ON.(2)24.
【解析】
试题分析:(1)根据四边形ABCD是菱形,判断出AD∥BC,AO=OC,即可推得OM=ON.
(2)首先根据四边形ABCD是菱形,判断出AC⊥BD,AD=BC=AB=5,进而求出BO、BD的值是多少;然后根据DE∥AC,AD∥CE,判断出四边形ACED是平行四边形,求出DE=AC=6,即可求出△BDE的周长是多少.
试题解析:(1)∵四边形ABCD是菱形,
∴AD∥BC,AO=OC,
∴![]() =1,
=1,
∴OM=ON.
(2)∵四边形ABCD是菱形,
∴AC⊥BD,AD=BC=AB=5,
∴BO=![]() =4,
=4,
∴BD=2BO=8,
∵DE∥AC,AD∥CE,
∴四边形ACED是平行四边形,
∴DE=AC=6,
∴△BDE的周长是:
BD+DE+BE
=BD+AC+(BC+CE)
=8+6+(5+5)
=24
即△BDE的周长是24.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1 ______ y2.(填“>”“<”或“=”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.
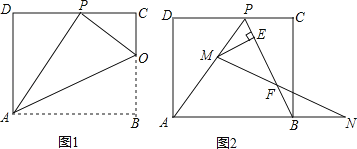
(1)如图1,已知折痕与边BC交于点O,连结AP、OP、OA.
①求证:△OCP∽△PDA;
②若△OCP与△PDA的面积比为1:4,求边AB的长;
(2)若图1中的点P恰好是CD边的中点,求∠OAB的度数;
(3)如图2,![]()
![]()
![]()
![]()
![]()
![]() ,擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.
,擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一枚棋子放在边长为1个单位长度的正六边形ABCDEF的顶点A处,通过摸球来确定该棋子的走法,其规则是:在一只不透明的袋子中,装有3个标号分别为1、2、3的相同小球,搅匀后从中任意摸出1个,记下标号后放回袋中并搅匀,再从中任意摸出1个,摸出的两个小球标号之和是几棋子就沿边按顺时针方向走几个单位长度.
棋子走到哪一点的可能性最大?求出棋子走到该点的概率.(用列表或画树状图的方法求解)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年山东省高考报名人数位居全国第三,约有696000人报名,将696000用科学记数法表示为( )
A.69.6×104
B.6.96×105
C.6.96×106
D.0.696×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
第一层 1+2=3
第二层 4+5+6=7+8
第三层 9+10+11+12=13+14+15
第四层 16+17+18+19+20=21+22+23+24
…
在上述的数字宝塔中,从上往下数,2017在第( )层.
A.41
B.45
C.43
D.44
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点B6的坐标是
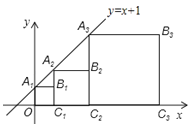
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们
除颜色外其余都相同.
(1)、求摸出1个球是白球的概率.
(2)、摸出1个球,记下颜色后放回,并搅匀,再摸出1个球并记下颜色.求两次摸出的球的颜色不同的概率(要求画树状图或列表).
(3)、现再将![]() 个白球放入布袋,搅匀后,使摸出1个球是白球的概率为
个白球放入布袋,搅匀后,使摸出1个球是白球的概率为![]() .求
.求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com