
 如图,△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当△EFG绕点D旋转时,点M运动的路径长为4π.
如图,△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当△EFG绕点D旋转时,点M运动的路径长为4π. 分析 如图,连接AD、DG.只要证明∠AMC=90°,即可解决问题.
解答 解:如图,连接AD、DG.
∵△ABC,△EFG均是边长为2的等边三角形,BD=CD,DE=DF,
∴AD⊥BC,GD⊥EF,
∴∠ADC=∠GDF=90°,
∴∠ADG=∠CDF,
∵AD=AG,DC=DF,
∴∠DAG=∠DGA=∠DCF=∠DFC,
∵∠DCF+∠DCM=180°,
∴∠DAM+∠DCM=180°,
∴∠ADC+∠AMC=180°,
∴∠AMC=90°,
∴点M的轨迹是以AC为直径的圆,
∴点M运动的路径长为4π,
故答案为4π.
点评 本题考查轨迹、等边三角形的性质、旋转变换、圆的有关知识,解题的关键是灵活运用所学知识解决问题,属于中考填空题中的压轴题.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
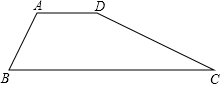 如图,已知四边形ABCD中,AD∥BC,AB=AD.
如图,已知四边形ABCD中,AD∥BC,AB=AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB、AC于E、F,已知EF∥BC.
如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB、AC于E、F,已知EF∥BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 35×104 | B. | 350×103 | C. | 3.5×105 | D. | 0.35×106 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com