
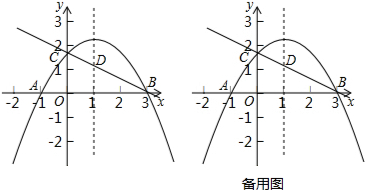
���� ��1�����������߹�A��B���㣬����ϵ�������ɵã�
��2������A��B��C��������ó���ABC���߳��ȣ��Ӷ��ж���ABCΪֱ���������ҡ�ABC=30�㣬���P������Ϊ��m��-$\frac{\sqrt{3}}{3}$m2+$\frac{2\sqrt{3}}{3}$m+$\sqrt{3}$��������P��PE��OB�ڵ�E����BE=3-m��PE=-$\frac{\sqrt{3}}{3}$m2+$\frac{2\sqrt{3}}{3}$m+$\sqrt{3}$�ɡ�DPB�ס�ACB֪��ABC=��DBP=30�㣬�ó���PBE=60�㣬�̶���tan��PBE=$\frac{PE}{BE}$���ó�����m�ķ��̣���֮�ɵã�
��3���ɵ�QΪ��O����ֱ��BC�ĶԳƵ�������Q�����꣬���ɵ�BQ�ij����ٷ�BQΪ���εıߺ�BQΪ���εĶԽ�����������ֱ���⣬����BQ�����εıߣ����N�ڹ���Q��ƽ����BC��ֱ���ϣ�����BQ=QN���������ľ��빫ʽ����ã�����BQ�����εĶԽ��ߣ��������ε�����BQ��MN���ഹֱƽ�֣��������BQ����ʽ���е�H�����꣬��MN��BQ���е�H������ɵ�MN�Ľ���ʽ�����ֱ��BC�Ľ���ʽ�ɵ�M������꣬�������MN�е�H�����꣬������õ�N�����꣮
��� �⣺��1����A��-1��0����B��3��0������y=ax2+bx+$\sqrt{3}$�У�
�ã�$\left\{\begin{array}{l}{a-b+\sqrt{3}=0}\\{9a+3b+\sqrt{3}=0}\end{array}\right.$����ã�$\left\{\begin{array}{l}{a=-\frac{\sqrt{3}}{3}}\\{b=\frac{2\sqrt{3}}{3}}\end{array}\right.$��
��������ߵı���ʽΪy=-$\frac{\sqrt{3}}{3}$x2+$\frac{2\sqrt{3}}{3}$x+$\sqrt{3}$��
��2����x=0ʱ��y=$\sqrt{3}$��
��C��0��$\sqrt{3}$����
��A��-1��0����B��3��0����
��AB=4��AC=2��BC=2$\sqrt{3}$��
��AB2=AC2+BC2��
���ACB=90�㣬
���ABCΪֱ�������Σ��ҡ�ABC=30�㣬
��ֱ��BC�Ľ���ʽΪy=kx+$\sqrt{3}$��
����B��3��0������y=kx+$\sqrt{3}$��
�ã�0=3k+$\sqrt{3}$����ã�k=-$\frac{\sqrt{3}}{3}$��
��ֱ��BC�Ľ���ʽΪy=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$��
��x=1ʱ��y=$\frac{2\sqrt{3}}{3}$��
��D��1��$\frac{2\sqrt{3}}{3}$����
���P��������m��-$\frac{\sqrt{3}}{3}$m2+$\frac{2\sqrt{3}}{3}$m+$\sqrt{3}$����
��ͼ1������P��PE��OB�ڵ�E��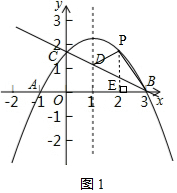
��BE=3-m��PE=-$\frac{\sqrt{3}}{3}$m2+$\frac{2\sqrt{3}}{3}$m+$\sqrt{3}$��
��Rt��ABC��
�ߡ�DPB�ס�ACB��
���ABC=��DBP=30�㣬
���PBE=60�㣬
��tan��PBE=$\frac{PE}{BE}$����$\frac{-\frac{\sqrt{3}}{3}{m}^{2}+\frac{2\sqrt{3}}{3}m+\sqrt{3}}{3-m}$=$\sqrt{3}$��
��ã�m=2��m=3���ᣩ��
���P��������2��$\sqrt{3}$����
��3���������⣬��ͼ2��ֱ��BC��ֱƽ��OQ����kBC=-$\frac{\sqrt{3}}{3}$��
��kOQ=$\sqrt{3}$��
��ֱ��OQ����ʽΪy=$\sqrt{3}$x����Q������Ϊ��a��$\sqrt{3}$a����
��OQ���е�F����Ϊ��$\frac{1}{2}$a��$\frac{\sqrt{3}}{2}$a����
����Q����ֱ��BC�Ľ���ʽΪy=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$���ã�-$\frac{\sqrt{3}}{6}$a+$\sqrt{3}$=$\frac{\sqrt{3}}{2}$a��
��ã�a=$\frac{3}{2}$��
��Q��$\frac{3}{2}$��$\frac{3\sqrt{3}}{2}$����
��BQ=$\sqrt{��\frac{3}{2}-3��^{2}+��0-\frac{3\sqrt{3}}{2}��^{2}}$=3��
�ٵ�BQ���ı���BQNM�ı�ʱ��
���ı���BQNM�����Σ�
��NQ��BC����NQ=BQ��
��kNQ=kBC=-$\frac{\sqrt{3}}{3}$��
��ֱ��NQ����ʽΪy=-$\frac{\sqrt{3}}{3}$��x-$\frac{3}{2}$��+$\frac{3\sqrt{3}}{2}$����y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$��
��N��m��-$\frac{\sqrt{3}}{3}$m+2$\sqrt{3}$����
��NQ=BQ����NQ2=BQ2�ɵã�m-$\frac{3}{2}$��2+��-$\frac{\sqrt{3}}{3}$m+2$\sqrt{3}$-$\frac{3\sqrt{3}}{2}$��2=9��
��ã�m=$\frac{3��3\sqrt{3}}{2}$��
��ʱ��N������Ϊ��$\frac{3+3\sqrt{3}}{2}$��$\frac{3\sqrt{3}-3}{2}$������$\frac{3-3\sqrt{3}}{2}$��$\frac{3\sqrt{3}+3}{2}$����
��MQ��BN����BN=BQ��
�������ε����ʿ�֪BM��ֱƽ��NQ��
���N���O�غϣ���N��0��0����
�ڵ�BQΪ�ı���BMQN�ĶԽ���ʱ��
���ı���BMQN�����Σ�
��BQ��MN���ഹֱƽ�֣�
��B��3��0����Q��$\frac{3}{2}$��$\frac{3\sqrt{3}}{2}$���ɵ�yBQ=-$\sqrt{3}$x+3$\sqrt{3}$��BQ�е�H��$\frac{9}{4}$��$\frac{3\sqrt{3}}{4}$����
��kMN=$\frac{\sqrt{3}}{3}$��
��yMN=$\frac{\sqrt{3}}{3}$��x-$\frac{9}{4}$��+$\frac{3\sqrt{3}}{4}$=$\frac{\sqrt{3}}{3}$x��
��$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{3}x}\\{y=-\sqrt{3}x+3\sqrt{3}}\end{array}\right.$�ɵõ�M��$\frac{3}{2}$��$\frac{\sqrt{3}}{2}$����
���N������m��n����
��M��N���е�H��$\frac{9}{4}$��$\frac{3\sqrt{3}}{4}$���ɵã�
$\left\{\begin{array}{l}{\frac{\frac{3}{2}+m}{2}=\frac{9}{4}}\\{\frac{\frac{\sqrt{3}}{2}+n}{2}=\frac{3\sqrt{3}}{4}}\end{array}\right.$����ã�$\left\{\begin{array}{l}{m=3}\\{n=\sqrt{3}}\end{array}\right.$��
����N��������3��$\sqrt{3}$����
���ϣ���N������Ϊ��$\frac{3+3\sqrt{3}}{2}$��$\frac{3\sqrt{3}-3}{2}$����$\frac{3-3\sqrt{3}}{2}$��$\frac{3\sqrt{3}+3}{2}$����0��0����3��$\sqrt{3}$����
���� ������Ҫ������κ�������Գơ����������ε����ʡ��ཻ�ߡ�ƽ����Ĺ�ϵ�����ε����ʣ��������������������֪ʶ���ǽ���Ĺؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4800��108 | B�� | 48��1010 | C�� | 4.8��103 | D�� | 4.8��1011 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
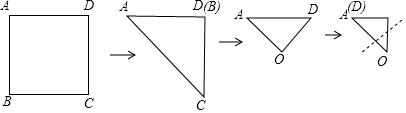
| A�� | ����ֱ�������� | B�� | ���� | C�� | ���� | D�� | ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
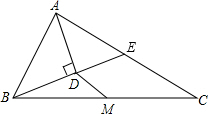 �ڡ�ABC�У���M�DZ�BC���е㣬ADƽ�֡�BAC��BD��AD��BD���ӳ��߽�AC�ڵ�E��AB=12��AC=20��
�ڡ�ABC�У���M�DZ�BC���е㣬ADƽ�֡�BAC��BD��AD��BD���ӳ��߽�AC�ڵ�E��AB=12��AC=20���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 20Ԫ | B�� | 24Ԫ | C�� | 30Ԫ | D�� | 36Ԫ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{a}{b}$=$\frac{a2}{b2}$ | B�� | $\frac{a}{b}$=$\frac{ab}{ab}$ | C�� | $\frac{a}{b}$=$\frac{a+2c}{b+2c}$��c��0�� | D�� | $\frac{a}{b}$=$\frac{ac}{bc}$ �� c��0 �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3��2��6 | B�� | 4��5��6 | C�� | 2��4��6 | D�� | 5��3��9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | 2 | C�� | -2 | D�� | $-\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com