
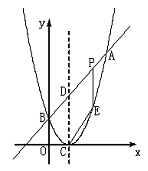
��ͼ����֪���κ���ͼ��Ķ�������ΪC(1,0)��ֱ��![]() ��ö��κ�����ͼ����A��B���㣬����A�������Ϊ(3,4)��B������
��ö��κ�����ͼ����A��B���㣬����A�������Ϊ(3,4)��B������![]() ��.��1����
��.��1����![]() ��ֵ��������κ����Ĺ�ϵʽ����2��PΪ�߶�AB�ϵ�һ�����㣨��P��A��B���غϣ�����P��
��ֵ��������κ����Ĺ�ϵʽ����2��PΪ�߶�AB�ϵ�һ�����㣨��P��A��B���غϣ�����P��![]() ��Ĵ�����������κ�����ͼ���ڵ�E�㣬���߶�PE�ij�Ϊ
��Ĵ�����������κ�����ͼ���ڵ�E�㣬���߶�PE�ij�Ϊ![]() ����P�ĺ�����Ϊ
����P�ĺ�����Ϊ![]() ����
����![]() ��
��![]() ֮��ĺ�����ϵʽ����д���Ա���
֮��ĺ�����ϵʽ����д���Ա���![]() ��ȡֵ��Χ����3��DΪֱ��AB��������κ���ͼ��Գ���Ľ��㣬���߶�AB���Ƿ����һ��P��ʹ���ı���DCEP��ƽ�����Σ������ڣ��������ʱP������ꣻ�������ڣ���˵������.
��ȡֵ��Χ����3��DΪֱ��AB��������κ���ͼ��Գ���Ľ��㣬���߶�AB���Ƿ����һ��P��ʹ���ı���DCEP��ƽ�����Σ������ڣ��������ʱP������ꣻ�������ڣ���˵������.
(1) �� ��A(3,4)��ֱ��y=x+m�ϣ��� 4=3+m. �� m=1.
��������κ����Ĺ�ϵʽΪy=a(x-1)2. �� ��A(3,4)�ڶ��κ���y=a(x-1)2��ͼ���ϣ� �� 4=a(3-1)2, �� a=1.
�� ������κ����Ĺ�ϵʽΪy=(x-1)2. ��y=x2-2x+1.
(2) ��P��E�����������ֱ�ΪyP��yE .�� PE=h=yP-yE =(x+1)-(x2-2x+1) =-x2+3x.
��h=-x2+3x (0��x��3).
(3) ����.Ҫʹ�ı���DCEP��ƽ���ı��Σ�������PE=DC. �� ��D��ֱ��y=x+1��,
�� ��D������Ϊ(1,2),�� -x2+3x=2 .��x2-3x+2=0 .
��֮���� x1=2��x2=1 (�������⣬��ȥ)
�� ��P�������Ϊ(2,3)ʱ���ı���DCEP��ƽ���ı���.


 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д� �������ϵ�д�
�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
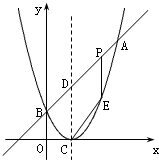 ��ͼ����֪���κ���ͼ��Ķ�������ΪC��1��0����ֱ��y=x+m��ö��κ�����ͼ����A��B���㣬����A�������Ϊ��3��4����B������y�ϣ�
��ͼ����֪���κ���ͼ��Ķ�������ΪC��1��0����ֱ��y=x+m��ö��κ�����ͼ����A��B���㣬����A�������Ϊ��3��4����B������y�ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
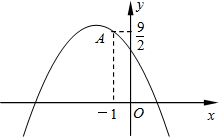 ��2012•�ߴ���һģ����ͼ����֪���κ���y=-
��2012•�ߴ���һģ����ͼ����֪���κ���y=-| 1 |
| 2 |
| 9 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
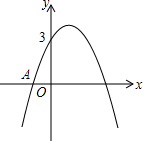 ��2013•��������ģ����ͼ����֪���κ���y=ax2+bx+3��ͼ�����A��-1��0�����Գ���Ϊ���㣨1��0������y��ƽ�е�ֱ�ߣ�
��2013•��������ģ����ͼ����֪���κ���y=ax2+bx+3��ͼ�����A��-1��0�����Գ���Ϊ���㣨1��0������y��ƽ�е�ֱ�ߣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����֪���κ���y=��x-1��2��ͼ��Ķ���ΪC�㣬ͼ����ֱ��y=x+m��ͼ����A��B���㣬����A�������Ϊ��3��4����B����y���ϣ�
��ͼ����֪���κ���y=��x-1��2��ͼ��Ķ���ΪC�㣬ͼ����ֱ��y=x+m��ͼ����A��B���㣬����A�������Ϊ��3��4����B����y���ϣ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com