
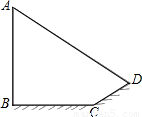
 (2010•鞍山)如图小明想测量电线杆AB的高度,发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4 m,BC=10 m,CD与地面成30°角,且此时测得1 m杆的影子长为2 m,则电线杆的高度约为 m.(结果保留两位有效数字,
(2010•鞍山)如图小明想测量电线杆AB的高度,发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4 m,BC=10 m,CD与地面成30°角,且此时测得1 m杆的影子长为2 m,则电线杆的高度约为 m.(结果保留两位有效数字, ≈1.41,
≈1.41,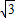 ≈1.73)
≈1.73) 
 ;
; ÷2=
÷2= .
. ≈8.7.
≈8.7.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源:2006年全国中考数学试题汇编《反比例函数》(04)(解析版) 题型:填空题
 ,5),D是AB边上的一点.将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,若点E在一反比例函数的图象上,那么该函数的解析式是 .
,5),D是AB边上的一点.将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,若点E在一反比例函数的图象上,那么该函数的解析式是 .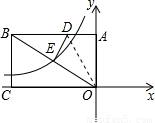
查看答案和解析>>
科目:初中数学 来源:2006年全国中考数学试题汇编《反比例函数》(03)(解析版) 题型:选择题
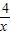 (x>0)的图象上,直角顶点A,B均在x轴上,则点B的坐标为( )
(x>0)的图象上,直角顶点A,B均在x轴上,则点B的坐标为( )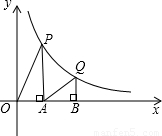
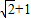 ,0)
,0)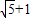 ,0)
,0)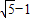 ,0)
,0)查看答案和解析>>
科目:初中数学 来源:2010年天津市中考数学模拟试卷(二)(解析版) 题型:填空题
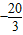 ,5),D是AB边上的一点.将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,若点E在一反比例函数的图象上,那么该函数的解析式是 .
,5),D是AB边上的一点.将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,若点E在一反比例函数的图象上,那么该函数的解析式是 .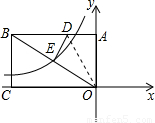
查看答案和解析>>
科目:初中数学 来源:2010年辽宁省鞍山市中考数学试卷(解析版) 题型:选择题
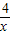 (x>0)的图象上,直角顶点A,B均在x轴上,则点B的坐标为( )
(x>0)的图象上,直角顶点A,B均在x轴上,则点B的坐标为( )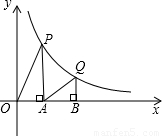
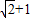 ,0)
,0) ,0)
,0)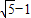 ,0)
,0)查看答案和解析>>
科目:初中数学 来源:2006年四川省乐山市中考数学试卷(课标卷)(解析版) 题型:选择题
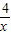 (x>0)的图象上,直角顶点A,B均在x轴上,则点B的坐标为( )
(x>0)的图象上,直角顶点A,B均在x轴上,则点B的坐标为( )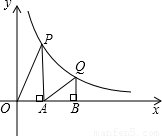
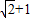 ,0)
,0)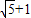 ,0)
,0)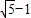 ,0)
,0)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com