已知a是正整数,如果关于x的方程x3+(a+17)x2+(38-a)x-56=0的根都是整数,求a的值及方程的整数根.
分析:先将原方程的左边分解因式,然后根据“两个数的乘积是0,其中最少有一个因式是0的”原则来分析;最后由二次方程的根的判别式及整数的奇偶性来解答.
解答:解:将方程的左边分解因式,得(x-1)【x
2+(a+18)x+56】=0,观察易知,方程有一个整数根x
1=1,
∵a是正整数,
∴关于x的方程x
2+(a+18)x+56=0(1)的判别式△=(a+18)
2-224>0,它一定有两个不同的实数根.
而原方程的根都是整数,所以方程(1)的根都是整数,因此它的判别式△=(a+18)
2-224应该是一个完全平方数.
设(a+18)
2-224=k
2(其中k为非负整数),则(a+18)
2-k
2=224,即(a+18+k)(a+18-k)=224.
显然a+18+k与a+18-k的奇偶性相同,且a+18+k≥18,而224=112×2=56×4=28×8,所以
或
或
解得
或
或
而a是正整数,所以只可能
或
当a=39时,方程(1)即x
2+57x+56=0,它的两根分别为-1和-56.此时原方程的三个根为1,-1和-56.
当a=12时,方程(1)即x
2+30x+56=0,它的两根分别为-2和-28.此时原方程的三个根为1,-2和-28
点评:本题综合考查了一元二次方程的整数根与有理根、因式分解的应用、一元二次方程的解与根的判别式等知识点,是难度比较大的一道题,在解题时,要分类讨论,勿漏解.



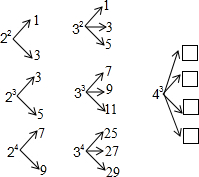 已知m≥2,n≥2,且m、n均为正整数,如果将mn进行如图所示的“分解”,那么下列四个叙述中正确的有( )
已知m≥2,n≥2,且m、n均为正整数,如果将mn进行如图所示的“分解”,那么下列四个叙述中正确的有( )