
【题目】如图,在△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D,点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA、AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s).
(1)求x为何值时,PQ⊥AC;
(2)设△PQD的面积为y(cm2),当0<x<2时,求y与x的函数关系式;
(3)当0<x<2时,求证:AD平分△PQD的面积;
(4)探索以PQ为直径的圆与AC的位置关系,请写出相应位置关系的x的取值范围(不要求写出过程).

【答案】(1)x=![]() ;(2)y=﹣
;(2)y=﹣![]() x2+
x2+![]() x;(3)证明见解析;(4)当0≤x<
x;(3)证明见解析;(4)当0≤x<![]() 或
或![]() <x<
<x<![]() 或
或![]() <x≤4时,以PQ为直径的圆与AC相交.
<x≤4时,以PQ为直径的圆与AC相交.
【解析】
(1)若使PQ⊥AC,则根据路程=速度×时间表示出CP和CQ的长,再根据30度的直角三角形的性质列方程求解;
(2)首先画出符合题意的图形,再根据路程=速度×时间表示出BP,CQ的长,根据等边三角形的三线合一求得PD的长,根据30度的直角三角形的性质求得PD边上的高,再根据面积公式进行求解;
(3)根据三角形的面积公式,要证明AD平分△PQD的面积,只需证明O是PQ的中点.根据题意可以证明BP=CN,则PD=DN,再根据平行线等分线段定理即可证明;
(4)根据(1)中求得的值即可分情况进行讨论.
(1)当Q在AB上时,显然PQ不垂直于AC,
当Q在AC上时,由题意得,BP=x,CQ=2x,PC=4﹣x;
∵AB=BC=CA=4,
∴∠C=60°;
若PQ⊥AC,则有∠QPC=30°,
∴PC=2CQ,
∴4﹣x=2×2x,
∴x=![]() ;
;
(2)y=﹣![]() x2+
x2+![]() x,
x,
如图所示,
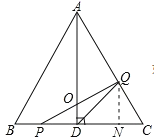
当0<x<2时,P在BD上,Q在AC上,过点Q作QN⊥BC于N;
∵∠C=60°,QC=2x,
∴QN=QC×sin60°=![]() x;
x;
∵AB=AC,AD⊥BC,
∴BD=CD=![]() BC=2,
BC=2,
∴DP=2﹣x,
∴y=![]() PDQN=
PDQN=![]() (2﹣x)
(2﹣x)![]() x=﹣
x=﹣![]() x2+
x2+![]() x;
x;
(3)当0<x<2时,
在Rt△QNC中,QC=2x,∠C=60°;
∴NC=x,
∴BP=NC,
∵BD=CD,
∴DP=DN;
∵AD⊥BC,QN⊥BC,
∴AD∥QN,
∴OP=OQ,
∴S△PDO=S△DQO,
∴AD平分△PQD的面积;
(4)显然,不存在x的值,使得以PQ为直径的圆与AC相离,
由(1)可知,当x=![]() 时,以PQ为直径的圆与AC相切;
时,以PQ为直径的圆与AC相切;
当点Q在AB上时,
8﹣2x=![]() ,
,
解得x=![]() ,
,
故当x=![]() 或
或![]() 时,以PQ为直径的圆与AC相切,
时,以PQ为直径的圆与AC相切,
当0≤x<![]() 或
或![]() <x<
<x<![]() 或
或![]() <x≤4时,以PQ为直径的圆与AC相交.
<x≤4时,以PQ为直径的圆与AC相交.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=(x+m)2+m与直线y=x相交于E,C两点(点E在点C的左边),抛物线与x轴交
于A,B两点(点A在点B的左边).△ABC的外接圆⊙H与直线y=-x相交于点D.
⑴ 若抛物线与y轴交点坐标为(0,2),求m的值;
⑵ 求证:⊙H与直线y=1相切;
⑶ 若DE=2EC,求⊙H的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,a),B(b,a),且a、b满足(a﹣2)2+|b﹣4|=0,现同时将点A,B分别向下平移2个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.

(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD;
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=![]() S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
(3)点P是直线BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合),直接写出∠BAP、∠DOP、∠APO之间满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC ∠ACB ,BD 、CD 分别平分△ABC 的内角 ∠ABC 、外角 ∠ACP ,BE平分外角 ∠MBC 交 DC 的延长线于点 E ,以下结论:①∠BDE ![]() ∠BAC ;② DB⊥BE ;③∠BDC ∠ACB 90 ;④∠BAC 2∠BEC 180 .其中正确的结论有( )
∠BAC ;② DB⊥BE ;③∠BDC ∠ACB 90 ;④∠BAC 2∠BEC 180 .其中正确的结论有( )
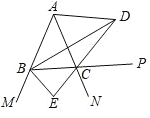
A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰直角三角形ABC,AB=AC,∠BAC=∠BDC=90°,

(1)若∠DBA=20°,则∠ACD=______°;
(2)连接AD,则∠ADB=______°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知命题“等腰三角形两腰上的高线长相等”
(1)请写出该命题的逆命题;
(2)判断(1)中命题的真假,并画出图形,补充已知,求证,及证明过程.
图形:
已知:在△ABC中,CD⊥AB,BE⊥AC,且______.
求证:______.
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料并把解答过程补充完整.
问题:在关于x,y的二元一次方程组![]() 中,x>1,y<0,求a的取值范围.
中,x>1,y<0,求a的取值范围.
在关于x,y的二元一次方程组中,利用参数a的代数式表示x,y,然后根据x>1,y<0列出关于参数a的不等式组即可求得a的取值范围.
解:由![]() ,解得
,解得 ,又因为x>1,y<0,所以
,又因为x>1,y<0,所以 ,解得________.
,解得________.
请你按照上述方法,完成下列问题:
已知x-y=4,x>3,y<1,求x+y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C在数轴上分别表示的数为-10,2,8,点D是BC中点,点E是AD中点.
(1)求EB的长;
(2)若动点P从点A出发,以1cm/s的速度向点C运动,达到点C停止运动,点Q从点C出发,以2cm/s的速度向点A运动,到达点A停止运动,若运动时间为ts,当t为何值时,PQ=3cm?
(3)点A,B,C开始在数轴上运动,若点A以1cm/s的速度向左运动,同时,点B和点C分别以4cm/s和9cm/s的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,请问:AB-BC的值是否随时间t的变化而变化?若变化,请说明理由;若不变,请求其常数值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com