练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．阅读下文，寻找规律：
    已知x≠1，计算：（1+x）（1-x）=1-x2，
    （1-x）（1+x+x2）=1-x3，
    （1-x）（1+x+x2+x3）=1-x4
    …
    （1）观察上式，猜想：（1-x）（1+x+x2+…+xn）=1-xn+1．
    （2）根据你的猜想，计算：
    ①（1-2）（1+2+22+…+22014）
    ②2+22+23+…+2n．

    分析 （1）由（1-x）（1+x）=1-x2，（1-x）（1+x+x2）=1-x3，（1-x）（1+x+x2+x3）=1-x4可以推出（1-x）（1+x+…+xn）=1-xn+1；
    （2）①利用（1）的规律得出答案即可；
    ②由得出规律的积除以因式即可．

    解答 解：（1）（1-x）（1+x+x2+…+xn）=1-xn+1；
    故答案为：1-xn+1；

    （2）①（1-2）（1+2+22+…+22014）
    =1-22014；
    ②2+22+23+24+…+2n=（1-2n+1）÷（1-2）-1=2n+1-2．

    点评 此题考查数字的变化规律，关键在于根据各式发现规律（1-x）（1+x+x2+…+xn）=1-xn+1，使等式左右两边的最大指数相同且左边是右边的因式分解得规律．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    19．计算或解方程
    （1）$（x-1{）^0}+{（\frac{1}{2}）^{-1}}+|{5-\sqrt{27}}|-2\sqrt{3}$
    （2）$（\sqrt{3}+\sqrt{2}）（\sqrt{3}-\sqrt{2}）-{（\sqrt{5}-\sqrt{2}）^2}$
    （3）x2-3x-1=0
    （4）9（x-2）2=4（x+1）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．（1）如图1，A（a，0）、B（b，0）且a、b满足|a+4|+$\sqrt{a+b}$=0
    ①求a、b的值；
    ②若C（-6，0），连CB，作BE⊥CB，垂足为B，且BC=BE，连AE交y轴于P，求P点坐标；
    （2）如图2，若A（6，0），B（0，3），点Q从A出发，以每秒1个单位的速度沿射线AO匀速运动，设点Q运动时间为t秒，过Q点作直线AB的垂线，垂足为D，直线QD与y轴交于E点，在点Q的运动过程中，一定存在△EOQ≌△AOB，请直接写出存在的t值以及相应的E点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图，点A和点B在数轴上

    （1）分别写出A、B两点表示的数；
    （2）在数轴上分别标出表示-1.5的C点，表示4.5的D点；
    （3）将A，B，C，D表示的有理数用“＜”连接起来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．计算
    （1）$\frac{{\sqrt{75}-\sqrt{3}}}{{\sqrt{3}}}-\sqrt{\frac{1}{5}}×\sqrt{20}$
    （2）$（\sqrt{6}-2\sqrt{15}）×\sqrt{3}-6\sqrt{\frac{1}{2}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．直线y=2x+k与y=6x-2的交点的横坐标为2，则k=6，交点为（2，10）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

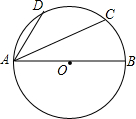    1．如图，A，B是⊙O的直径，C、D在⊙O上，$\widehat{AD}$=$\widehat{DC}$，若∠DAB=58°，则∠CAB=（　　）
    A．20°B．22°C．24°D．26°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．请你观察下列各式，用含自然数n（n≧1）的代数式填空，并在表格右侧说明你的理由？
    $\sqrt{1+\frac{1}{3}}$=2$\sqrt{\frac{1}{3}}$理由：
    $\sqrt{2+\frac{1}{4}}$=3$\sqrt{\frac{1}{4}}$
    $\sqrt{3+\frac{1}{5}}$=4$\sqrt{\frac{1}{5}}$
            …
    $\sqrt{n+\frac{1}{n+2}}$=（n+1）$\sqrt{\frac{1}{n+2}}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．某游泳馆普通票价20元/张，暑期为了促销，新推出了两种优惠卡：
    A卡：售价300元/张，每次凭卡另收5元；
    B卡：售价150元/张，每次凭卡另收10元．
    （1）若暑假游泳x次，请你分别写出普通票正常出售、办A卡、办B卡三种方式所需总费用；
    （2）小明假期打算游泳健身，估计游泳次数为40次，你认为采用哪种方式较为合算？

    查看答案和解析>>

    同步练习册答案