
【题目】如图1,在矩形ABCD中,P为CD边上一点(DP<CP),∠APB=90°.M在AB上,且∠APM=∠APD,过点B作BN∥MP交DC于点N.
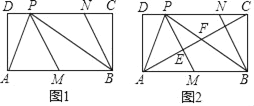
(1)求证:四边形PMBN是菱形;
(2)求证:ADBC=DPPC;
(3)如图2,连接AC,分别交PM,PB于点E,F,若DP=1,AD=2,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
(1)DP∥AB,所以∠DPA=∠PAM,由题意可知:∠DPA=∠APM,所以∠PAM=∠APM,由于∠APB﹣∠PAM=∠APB﹣∠APM,即∠ABP=∠MPB,从而可知PM=MB=AM,又易证四边形PMBN是平行四边形,所以四边形PMBN是菱形;
(2)根据余角的性质得到∠DAP=∠BPC,根据相似三角形的性质即可得到结论;
(3)根据矩形的性质得到BC=AD=2,求得AB=CD=5,根据平行线的性质得到∠APD=∠PAM,推出AM=MP,得到AM=MB=![]() ,根据相似三角形的性质得到
,根据相似三角形的性质得到![]() ,求得
,求得![]() ,根据相似三角形的性质得到
,根据相似三角形的性质得到![]() ,得到
,得到![]() ,于是得到结论.
,于是得到结论.
(1)证明:在矩形ABCD中,DC∥AB,
∵BN∥MP,
∴四边形PMBN是平行四边形,
∵∠APB=90°,
∴∠APM+∠BPM=90°,
∠APD+∠BPC=90°,
∵∠APM=∠APD,
∴∠BPM=∠BPC,
∵DC∥AB,
∴∠BPC=∠PBM,
∵∠BPM=∠PBM
∴MP=MB,
∴平行四边形PMBN是菱形;
(2)证明:在矩形ABCD中,∠D=∠C=90°,
∴∠APD+∠DAP=90°,
∵∠APD+∠BPC=90°,
∴∠DAP=∠BPC,
∴△ADP∽△PCB,
∴![]() ,
,
∴ADBC=DPPC;
(3)解:∵四边形ABCD是矩形,
∴BC=AD=2,
由(2)得ADBC=DPPC
∴PC=4,
∴AB=CD=5,
在矩形ABCD中,DC∥AB,
∴∠APD=∠PAM,
∵∠APM=∠APD,
∴∠PAM=∠APM,
∴AM=MP,
由(1)得MP=MB,
∴AM=MB=![]() ,
,
∵DC∥AB,
∴∠PCA=∠CAB,
∵∠PFC=∠BFA,
∴△PCF∽△BAF,
∴![]() ,
,
∴![]() ,
,
同理可得△PCE∽△MAE,
∴![]() ,
,
∴![]() ,
,
∴EF=AC﹣CF﹣AE=![]() AC,
AC,
∴ .
.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD,将边CD绕点C顺时针旋转60°,得到线段CE,连接DE,AE,BD交于点F.
(1)求∠AFB的度数;
(2)求证:BF=EF;
(3)连接CF,直接用等式表示线段AB,CF,EF的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
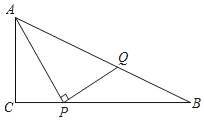
【题目】如图,Rt△ABC中,∠C=90°,P是CB边上一动点,连接AP,作PQ⊥AP交AB于Q.已知AC=3cm,BC=6cm,设PC的长度为xcm,BQ的长度为ycm.
小青同学根据学习函数的经验对函数y随自变量x的变化而变化的规律进行了探究.
下面是小青同学的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y的几组对应值;
x/cm | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 6 |
y/cm | 0 | 1.56 | 2.24 | 2.51 | m | 2.45 | 2.24 | 1.96 | 1.63 | 1.26 | 0.86 | 0 |
(说明:补全表格时,相关数据保留一位小数)
m的值约为多少cm;
(2)在平面直角坐标系中,描出以补全后的表格中各组数值所对应的点(x,y),画出该函数的图象;
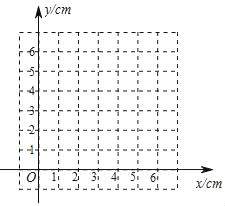
(3)结合画出的函数图象,解决问题:
①当y>2时,写出对应的x的取值范围;
②若点P不与B,C两点重合,是否存在点P,使得BQ=BP?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在测量“河流宽度”的综合与实践活动中,小李同学设计的方案及测量数据如下:在河对岸边选定一个目标点A,在近岸取点B,C,D (点B,C,D在同一条直线上),AB⊥BD,∠ACB=45°,CD=20米,且.若测得∠ADB=25°,请你帮助小李求河的宽度AB.(sin25°≈0.42,cos25°≈0.91,tan25°≈0.47,结果精确到0.1米).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
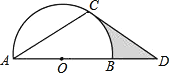
【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com