Question

18．综合与实践：制作礼品盒
如图（1），小颖将边长为60cm的正方形硬纸片ABCD，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，如图（2），点A，B，C，D四点重合于点P，做成一个底面是正方形的长方体形状的礼品盒．设礼品盒的侧面积为Scm²，AE=FB=xcm．

（1）求S与x之间的关系式及S的最大值；
（2）小颖有一底面半径为15cm，高为15cm的圆柱体形状的礼品，该礼品能否底面朝下放入她做成的礼品盒？若能，求出x的值；若不能，请说明理由．

Answer 1

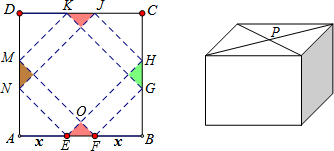
分析 （1）根据条件可以分别表示出阴影部分的面积，掀起的四个角上的四个等腰直角三角形的面积之和及底部正方形的面积就可以表示出S与x之间的函数关系式；将解析式化为顶点式就可以求出S的最大值；
（2）设包装盒的底面正方形的边长为a，高为h，就可以得出AE=$\frac{\sqrt{2}}{2}$a，EF=60-2AE=60-$\sqrt{2}$a，h=$\frac{\sqrt{2}}{2}$EF=30$\sqrt{2}$-a，再三种情况讨论就可以得出结论．

解答 解：（1）∵AE=FB=xcm，
∴EF的长为（60-2x）cm．
图中阴影部分拼在一起是边长为EF的正方形，其面积为：（60-2x）²cm²，
掀起的四个角上的四个等腰直角三角形的面积之和为：2x²cm²；
盒底正方形的边长为$\sqrt{2}$x，其面积为2x²；
∴S=60²-（60-2x）²-4x²=240x-8x²
∴S=-8（x²-30x）=-8（x-15）²+1800（0＜x＜30），
∵a=-8＜0．
∴抛物线的开口向下，S有最大值．
∴x=15cm时，侧面积最大为1800cm²，
答：若包装盒侧面积S_最大=1800cm²最大，x应取15cm．

（2）包装盒的底面正方形的边长为a，高为h，
∴AE=$\frac{\sqrt{2}}{2}$a，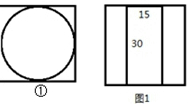
∴EF=60-2AE=60-$\sqrt{2}$a，
∴h=$\frac{\sqrt{2}}{2}$EF=30$\sqrt{2}$-a，
∴包装盒的高h随底面边长的增大而减小．
圆柱的底面朝下放入，此时包装盒高h不能小于15．
∵圆柱的底面半径为15cm，
∴盒底边长最小取30cm（放入如①图），
∴h=30$\sqrt{2}$-a=30（$\sqrt{2}$-1）＜15，故不能放下．

点评 本题考查了勾股定理的运用，矩形的面积的运用，正方形的性质的运用，二次函数的解析式的运用，分类讨论思想的运用，解答时分类讨论是难点．