
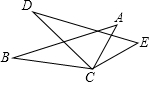
 如图,已知∠B=∠D,AB=DE,要推得△ABC≌△EDC;
如图,已知∠B=∠D,AB=DE,要推得△ABC≌△EDC;分析 (1)根据全等三角形的判定定理SAS,结合给定条件以及图形即可找出另一对相等的边;
(2)根据全等三角形的判定定理ASA,结合给定条件以及图形即可找出另一对相等的角;
(3)根据全等三角形的判定定理AAS,结合给定条件以及图形即可找出另一对相等的角.
解答 解:(1)∵∠B=∠D,AB=ED,
当BC=DC时,在△ABC和△EDC中,$\left\{\begin{array}{l}{AB=ED}\\{∠B=∠D}\\{BC=DC}\end{array}\right.$,
∴△ABC≌△EDC(SAS).
故答案为:BC=DC.
(2)∵∠B=∠D,AB=ED,
当∠A=∠E时,在△ABC和△EDC中,$\left\{\begin{array}{l}{∠B=∠D}\\{AB=ED}\\{∠A=∠E}\end{array}\right.$,
∴△ABC≌△EDC(ASA).
故答案为:∠A=∠E.
(3)∵∠B=∠D,AB=ED,
当∠ACB=∠ECD时,在△ABC和△EDC中,$\left\{\begin{array}{l}{∠B=∠D}\\{∠ACB=∠ECD}\\{AB=ED}\end{array}\right.$,
∴△ABC≌△EDC(AAS).
故答案为:∠ACB=∠ECD.
点评 本题考查了全等三角形的判定,熟练掌握全等三角形的各判定定理是解题的关键.


科目:初中数学 来源: 题型:选择题
 A、B两市相距260千米,甲车从A市前往B市运送物资,行驶2小时到达M地,发现汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间不计),乙车到达M地后用20分钟修好甲车,又以原速原路返回,同时甲车以原来1.5倍的速度前往B市.如图时两车相距A市的路程y(单位:千米)与甲车行驶时间(单位:小时)之间的函数图象,下列四中说法:
A、B两市相距260千米,甲车从A市前往B市运送物资,行驶2小时到达M地,发现汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间不计),乙车到达M地后用20分钟修好甲车,又以原速原路返回,同时甲车以原来1.5倍的速度前往B市.如图时两车相距A市的路程y(单位:千米)与甲车行驶时间(单位:小时)之间的函数图象,下列四中说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1道 | B. | 2道 | C. | 3道 | D. | 4道 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com