
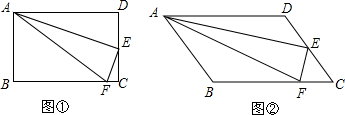
分析 探究:延长AE交BC的延长线与G,由矩形的性质得出∠DAE=∠G,由AAS证明△ADE≌△GCE,得出AE=GE,AD=GC,由已知条件得出∠G=∠FAE,证出AF=GF,再由等腰三角形的三线合一性质即可得出结论;
拓展:延长AE交BC的延长线与G,由平行四边形的性质得出∠DAE=∠G,由AAS证明△ADE≌△GCE(AAS),得出AE=GE,AD=GC,证出∠G=∠FAE,得出AF=GF,由等腰三角形的性质得出AE⊥EF,求出AF=GF=CF+CG=CF+AD=3,由三角函数得出isn∠DAE=sjn∠FAE=$\frac{EF}{AF}$=$\frac{1}{5}$即可.
解答 探究: 解:AE⊥EF;理由如下:
解:AE⊥EF;理由如下:
延长AE交BC的延长线与G,如图1所示:
∵E是CD的中点,
∴DE=CE,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAE=∠G,
在△ADE和△GCE中,
$\left\{\begin{array}{l}{∠DAE=∠G}&{\;}\\{∠AED=∠GEC}&{\;}\\{DE=CE}&{\;}\end{array}\right.$,
∴△ADE≌△GCE(AAS),
∴AE=GE,AD=GC,
∵∠DAE=∠FAE,
∴∠G=∠FAE,
∴AF=GF,
∵AE=GE,
∴AE⊥EF;
拓展: 解:延长AE交BC的延长线与G,如图1所示:
解:延长AE交BC的延长线与G,如图1所示:
∵E是CD的中点,
∴DE=CE,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠G,
在△ADE和△GCE中,
$\left\{\begin{array}{l}{∠DAE=∠G}&{\;}\\{∠AED=∠GEC}&{\;}\\{DE=CE}&{\;}\end{array}\right.$,
∴△ADE≌△GCE(AAS),
∴AE=GE,AD=GC,
∵∠DAE=∠FAE,
∴∠G=∠FAE,
∴AF=GF,
∵AE=GE,
∴AE⊥EF,
∴∠AEF=90°,
∵AF=GF=CF+CG=CF+AD=$\frac{1}{2}$+$\frac{5}{2}$=3,
∴sin∠DAE=sin∠FAE=$\frac{EF}{AF}$=$\frac{\frac{3}{5}}{3}$=$\frac{1}{5}$.
故答案为:$\frac{1}{5}$.
点评 本题考查了矩形的性质、平行四边形的性质、全等三角形的判定与性质、等腰三角形的判定与性质、三角函数等知识;熟练掌握矩形和平行四边形的性质,证明三角形全等是解决问题的关键.


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
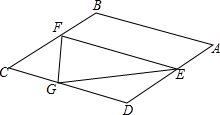 如图,在菱形ABCD中,AB=$\sqrt{3}$,∠B=120°,E是AD边上的一个动点(不与点A,D重合),EF∥AB交BC于点F,点G在CD上,DG=DE.
如图,在菱形ABCD中,AB=$\sqrt{3}$,∠B=120°,E是AD边上的一个动点(不与点A,D重合),EF∥AB交BC于点F,点G在CD上,DG=DE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=1 | B. | x=-1 | C. | x=$\frac{3}{5}$ | D. | 无解 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
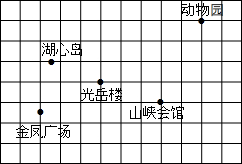 如图是某市市区几个旅游景点的示意图(图中每个小正方形的边长都为1个单位长度).建立适当的平面直角坐标系,使光岳楼的坐标为(-1,0),并用坐标表示下列景点的位置.
如图是某市市区几个旅游景点的示意图(图中每个小正方形的边长都为1个单位长度).建立适当的平面直角坐标系,使光岳楼的坐标为(-1,0),并用坐标表示下列景点的位置.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com