
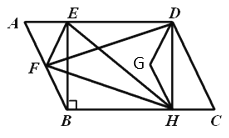
【题目】如图,已知![]() ,
,![]() 于
于![]() ,
,![]() 为
为![]() 中点,连接
中点,连接![]() ,将
,将![]() 向右平移到
向右平移到![]() ,使
,使![]() 与
与![]() 重合,
重合,![]() 与
与![]() 重合,
重合,![]() 与
与![]() 重合,连接
重合,连接![]() ,
,![]() ,
,![]() ,若
,若![]() 为
为![]() 的高的交点,
的高的交点,![]() ,
,![]() ,则
,则![]() 到
到![]() 的距离为________.
的距离为________.
【答案】3
【解析】
延长HG交FD于N点,过F点作FM⊥EH,由直角三角形斜边中线性质得AF=EF=BF,利用平移、等腰三角形性质、垂直等条件证明角相等从而可得![]() ,根据相似三角形性质求出AF长,再由勾股定理即可求出BE、FD、EH等线段长,有勾股定理逆定理证明
,根据相似三角形性质求出AF长,再由勾股定理即可求出BE、FD、EH等线段长,有勾股定理逆定理证明![]() 是直角三角形,从而由三角形面积求出斜边的高.
是直角三角形,从而由三角形面积求出斜边的高.
解:延长HG交FD于N点,过F点作FM⊥EH,
∵![]() 于
于![]() ,即∠BED=∠EBH=90°,
,即∠BED=∠EBH=90°,![]() 为
为![]() 中点,
中点,
∴AF=EF=BF,
∴∠FEB=∠FBE,∠FAE=∠FEA,
由平移性质可知:∠HDE=∠DHB=90°,∠GHD=∠GDH=∠FEB=∠FBE,∠AEF=∠GDA,
∴四边形BHDE是矩形,
∴BH=DE=8,
∵![]() 为
为![]() 的高的交点,
的高的交点,
∴∠GHD+∠FDH=90°,
又∵∠FDH+∠FDA=90°,
∴∠FDA=∠GHD,
∴∠FDA=∠ABE,
∴∠AFD=∠AEB=90°,
又∵∠A=∠A,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
∴在![]() 中,
中,![]()
在![]() 中,
中,![]()
在![]() 中,
中,![]()
易证![]()
∴在![]() 中
中![]() ,
,
∴![]() 是直角三角形,∠EFH=90°,
是直角三角形,∠EFH=90°,
∴![]() ,即
,即![]() ,
,
∴![]() .即
.即![]() 到
到![]() 的距离为3.
的距离为3.
故答案为:3.


科目:初中数学 来源: 题型:
【题目】已知关于x,y的方程组![]() ,给出下列结论:
,给出下列结论:
①![]() 是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;③当a=1时,方程组的解也是方程x+y=4a的解;④x,y的都为自然数的解有4对.其中正确的个数为_____.
是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;③当a=1时,方程组的解也是方程x+y=4a的解;④x,y的都为自然数的解有4对.其中正确的个数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
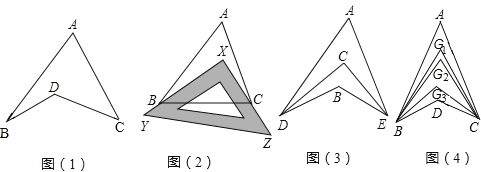
【题目】探究与发现:如图1所示的图形,像我们常见的学习用品﹣﹣圆规.我们不妨把这样图形叫做“规形图”.
(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,∠A=40°,则∠ABX+∠ACX= °;
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数;
③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=133°,∠BG1C=70°,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了缅怀先烈.继承遗志,某中学初二年级同学于4月初进行“清明雁栖湖,忆先烈功垂不朽”的定向越野活动每个小组需要在点![]() 出发,跑步到点
出发,跑步到点![]() 打卡(每小组打卡时间为1分钟),然后跑步到
打卡(每小组打卡时间为1分钟),然后跑步到![]() 点,……最后到达终点(假设点
点,……最后到达终点(假设点![]() ,点
,点![]() ,点
,点![]() 在一条直线上,且在行进过程中,每个小组跑步速度是不变的),“文艺组”最先出发.过了一段时间后,“方程组”开始出发,两个小组恰好同时到达点
在一条直线上,且在行进过程中,每个小组跑步速度是不变的),“文艺组”最先出发.过了一段时间后,“方程组”开始出发,两个小组恰好同时到达点![]() .若“方程组”出发的时间为
.若“方程组”出发的时间为![]() (单位:分钟),在点
(单位:分钟),在点![]() 与点
与点![]() 之间的行进过程中,“文艺组”和“方程组”之间的距离为
之间的行进过程中,“文艺组”和“方程组”之间的距离为![]() (单位:米),它们的函数图像如下图:则下面判断不正确的是( )
(单位:米),它们的函数图像如下图:则下面判断不正确的是( )
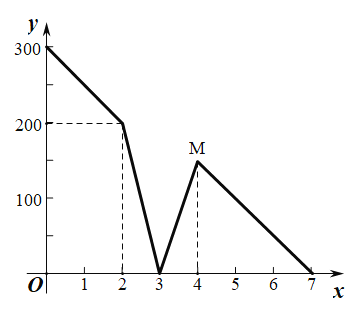
A.当![]() 时,“文艺组”恰好到达
时,“文艺组”恰好到达![]() 点;
点;
B.“文艺组”的速度为150米/分钟,“方程组”的速度为200米/分钟他们从![]() 点出发的时间间隔为2分钟
点出发的时间间隔为2分钟
C.图中![]() 点表示“方程组”在
点表示“方程组”在![]() 点打卡结束,开始向
点打卡结束,开始向![]() 点出发;
点出发;
D.出发点![]() 到打卡点
到打卡点![]() 的距离是600米,打卡点
的距离是600米,打卡点![]() 到点
到点![]() 的距离是800米
的距离是800米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在同一个平面内,![]() ,
,![]() .
.
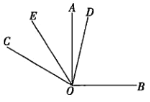
(1)填空:![]() ________;
________;
(2)如果OD平分![]() ,OE平分
,OE平分![]() ,那么
,那么![]() 的度数为;
的度数为;
(3)试问在(2)的条件下,如果将题目中![]() 改为
改为![]() ,其他条件不变,你能求出
,其他条件不变,你能求出![]() 的度数吗?若能,请你写出求解过程;若不能,请说明理由.
的度数吗?若能,请你写出求解过程;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】智能手环是一种穿戴式智能设备,通过智能手环,用户可以记录日常生活中的锻炼,睡眠、部分还有饮食等实时数据,并将这些数据与手机、平板同步,起到通过数据指导健康生活的作用,某公司2020年3月新推出![]() 型和
型和![]() 型两款手环.
型两款手环.![]() 型手环每只售价是
型手环每只售价是![]() 型手环售价的1.5倍.3月份
型手环售价的1.5倍.3月份![]() 、
、![]() 手环总计销售650只,
手环总计销售650只,![]() 型手环销售额为108000元,
型手环销售额为108000元,![]() 型手环销售额为84000元.
型手环销售额为84000元.
(1)求![]() 、
、![]() 型手环的售价各是多少?
型手环的售价各是多少?
(2)由于更多的公司研发手环投入市场,市场竞争的加剧,公司决定4月份对两种手环进行降价促销,对![]() 型手环直降
型手环直降![]() 元,销量比原来提高了
元,销量比原来提高了![]() ,对
,对![]() 型手环在原价基础上降价
型手环在原价基础上降价![]() 销售,销量比原来提高了20%,4月份总计销售额为208320元,求
销售,销量比原来提高了20%,4月份总计销售额为208320元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据![]() 单位:米
单位:米![]() ,解答下列问题:
,解答下列问题:
![]() 用含m,n的代数式表示地面的总面积S;
用含m,n的代数式表示地面的总面积S;
![]() 已知客厅面积是卫生间面积的8倍,且卫生间、卧室、厨房面积的和比客厅还少3平方米,如果铺1平方米地砖的平均费用为100元,那么小李铺地砖的总费用为多少元?
已知客厅面积是卫生间面积的8倍,且卫生间、卧室、厨房面积的和比客厅还少3平方米,如果铺1平方米地砖的平均费用为100元,那么小李铺地砖的总费用为多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2mx+4m﹣8,
(1)当x≤2时,函数值y随x的增大而减小,求m的取值范围.
(2)以抛物线y=x2﹣2mx+4m﹣8的顶点A为一个顶点作该抛物线的内接正三角形AMN(M,N两点在拋物线上),请问:△AMN的面积是与m无关的定值吗?若是,请求出这个定值;若不是,请说明理由.
(3)若抛物线y=x2﹣2mx+4m﹣8与x轴交点的横坐标均为整数,求整数m的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在直角坐标平面内,抛物线y=x2+bx+c经过点A(2,0)、B(0,6).
(1)求抛物线的表达式;
(2)抛物线向下平移几个单位后经过点(4,0)?请通过计算说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com