
【题目】如图,在函数y1=![]() (x<0)和y2=
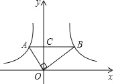
(x<0)和y2=![]() (x>0)的图象上,分别有A、B两点,若AB∥x轴,交y轴于点C,且OA⊥OB,S△AOC=
(x>0)的图象上,分别有A、B两点,若AB∥x轴,交y轴于点C,且OA⊥OB,S△AOC=![]() ,S△BOC=
,S△BOC=![]() ,则线段AB的长度=__.
,则线段AB的长度=__.
【答案】![]()
【解析】
已知S△AOC=![]() ,S△BOC=
,S△BOC=![]() ,根据反比例函数k的几何意义可得k1=﹣1,k2=9,即可得两反比例解析式为y=﹣
,根据反比例函数k的几何意义可得k1=﹣1,k2=9,即可得两反比例解析式为y=﹣![]() ,y=
,y=![]() ;设B点坐标为(
;设B点坐标为(![]() ,t)(t>0),由AB∥x轴,可得A点的纵坐标为t,代入y=﹣
,t)(t>0),由AB∥x轴,可得A点的纵坐标为t,代入y=﹣![]() 求得A点坐标为(﹣
求得A点坐标为(﹣![]() ,t);再证明Rt△AOC∽Rt△OBC,根据相似三角形的性质可得OC:BC=AC:OC,代入数据可得t:
,t);再证明Rt△AOC∽Rt△OBC,根据相似三角形的性质可得OC:BC=AC:OC,代入数据可得t:![]() =
=![]() :t,解得t=
:t,解得t=![]() ,由此可得A点坐标为(﹣
,由此可得A点坐标为(﹣![]() ,
,![]() ),B点坐标为(3
),B点坐标为(3![]() ,
,![]() ),即可求得线段AB的长度.
),即可求得线段AB的长度.
∵S△AOC=![]() ,S△BOC=
,S△BOC=![]() ,
,
∴![]() |k1|=
|k1|=![]() ,
,![]() |k2|=
|k2|=![]() ,
,
∴k1=﹣1,k2=9,
∴两反比例解析式为y=﹣![]() ,y=
,y=![]() ,
,
设B点坐标为(![]() ,t)(t>0),
,t)(t>0),
∵AB∥x轴,
∴A点的纵坐标为t,
把y=t代入y=﹣![]() 得x=﹣
得x=﹣![]() ,
,
∴A点坐标为(﹣![]() ,t),
,t),
∵OA⊥OB,
∴∠AOC=∠OBC,
∴Rt△AOC∽Rt△OBC,
∴OC:BC=AC:OC,即t:![]() =
=![]() :t,
:t,
∴t=![]() ,
,
∴A点坐标为(﹣![]() ,
,![]() ),B点坐标为(3
),B点坐标为(3![]() ,
,![]() ),
),
∴线段AB的长度=3![]() ﹣(﹣
﹣(﹣![]() )=
)=![]() .
.
故答案为:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】发现与探索
小丽发现通过用两种不同的方法计算同一几何体体积,就可以得到一个恒等式.如图是边长为![]() 的正方体,被如图所示的分割线分成
的正方体,被如图所示的分割线分成![]() 块.
块.

![]() ;
;
![]() ;
;
![]() 用不同的方法计算这个正方体的体积,就可以得到一个等式,这个等式为:________;
用不同的方法计算这个正方体的体积,就可以得到一个等式,这个等式为:________;
![]() 已知
已知![]() ,
,![]() ,利用上面的规律求
,利用上面的规律求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,A、B两个顶点在![]() 轴的上方,点C的坐标是(1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a,则点B的横坐标是( )
轴的上方,点C的坐标是(1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a,则点B的横坐标是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红的父母开了一个小服装店,出售某种进价为![]() 元的服装,现每件
元的服装,现每件![]() 元,每星期可卖
元,每星期可卖![]() 件.该同学对市场作了如下调查:每降价
件.该同学对市场作了如下调查:每降价![]() 元,每星期可多卖
元,每星期可多卖![]() 件;每涨价
件;每涨价![]() 元,每星期要少卖
元,每星期要少卖![]() 件.
件.
![]() 小红已经求出在涨价情况下一个星期的利润
小红已经求出在涨价情况下一个星期的利润![]() (元)与售价
(元)与售价![]() (元)(
(元)(![]() 为整数)的函数关系式为
为整数)的函数关系式为![]() ,请你求出在降价的情况下
,请你求出在降价的情况下![]() 与
与![]() 的函数关系式;
的函数关系式;
![]() 在降价的条件下,问每件商品的售价定为多少时,一个星期的利润恰好为
在降价的条件下,问每件商品的售价定为多少时,一个星期的利润恰好为![]() 元?
元?
![]() 问如何定价,才能使一星期获得的利润最大?
问如何定价,才能使一星期获得的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
如图,在△ABC中,点E、D、F分别在边AB、BC、CA上,且DE∥CA,DF∥BA.下列四个判断中,不正确的是( )
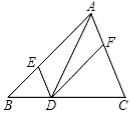
A.四边形AEDF是平行四边形
B.如果∠BAC=90°,那么四边形AEDF是矩形
C.如果AD平分∠BAC,那么四边形AEDF是矩形
D.如果AD⊥BC且AB=AC,那么四边形AEDF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
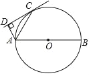
【题目】如图,AB是⊙O的直径,C是⊙O上一点,AC平分∠DAB,AD⊥CD于D.
(1)求证:直线CD是⊙O的切线;
(2)若AB=10,sin∠ACD=![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正五边形的边长为2,连接对角线AD,BE,CE.线段AD分别与BE,CE相交于点M,N.给出下列结论:①△ABM≌△DCN;②DM2=DNAD;③MN=3+![]() ;④四边形ANCB为菱形.其中正确的是_____
;④四边形ANCB为菱形.其中正确的是_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y-2与x+2成正比例,且x=1时,y=8.
解答:⑴求y与x之间的函数关系式;
⑵ 在平面直角坐标系中,① 画出 ⑴ 中的y与x之间的函数关系式的图像;
②若将此图像绕着原点O逆时针转90°,求出此图像的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:在以后你的学习中,我们会学习一个定理:直角三角形斜边上的中线等于斜边的一半,即:如图1,在Rt△ABC中,∠ACB=90°,若点D是斜边AB的中点,则CD=![]() AB.
AB.

灵活应用:如图2,△ABC中,∠BAC=90°,AB=3, AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连接BE, CE.
(1)求AD的长;
(2)判断△BCE的形状;
(3)求CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com