
【题目】如图,已知MON=30°,OA=4,在OM、ON上分别找一点B、C,使AB+BC最小,则最小值为___________.

【答案】![]()
【解析】
作点A关于OM的对称点A',过A'作A'C⊥ON于C,交OM于点B,则AB+BC最小.由轴对称性质可得:A'B=AB,A'D=AD,根据直角三角形两锐角互余得到∠A'AO=60°,∠A'=30°,再根据30°角所对直角边等于斜边的一半即可求出AD,AC的长,进而可求出结论.
如图所示,作点A关于OM的对称点A',过A'作A'C⊥ON于C,交OM于点B,则B、C即为所求的点.
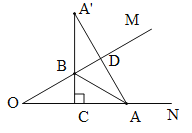
由轴对称性质可得:A'B=AB,A'D=AD.
∵∠MON=30°,∴∠A'AO=60°.
∵OA=4,∴A'D=AD=2.
∵∠CAA'=60°,∠A'CA=90°,∴∠A'=30°,∴AC=![]() AA'=AD=2,A'C=
AA'=AD=2,A'C=![]() AC=
AC=![]() .
.
∵AB=A'B,∴AB+BC=A'C=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2,BC=4.将矩形ABCD绕点C沿顺时针方向旋转90°后,得到矩形FGCE(点A、B、D的对应点分别为点F、G、E).动点P从点B开始沿BC-CE运动到点E后停止,动点Q从点E开始沿EF-FG运动到点G后停止,这两点的运动速度均为每秒1个单位.若点P和点Q同时开始运动,运动时间为x(秒),△APQ的面积为y,则能够正确反映y与x之间的函数关系的图象大致是( )

A. 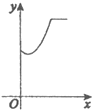 B.
B. 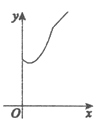 C.
C. 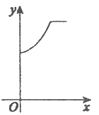 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于A、B两点,点P在函数
轴交于A、B两点,点P在函数![]() 的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( ).
的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( ).
A. 2个 B. 3个 C. 4个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 抛物线![]() 与
与![]() 轴交于点A(-1,0),顶点坐标(1,n)与
轴交于点A(-1,0),顶点坐标(1,n)与![]() 轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①
轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数m,
;③对于任意实数m,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 有两个不相等的实数根.其中结论正确的个数为
有两个不相等的实数根.其中结论正确的个数为![]()
![]()

A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
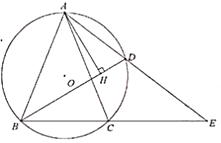
【题目】如图,△ABC内接于⊙O,![]() ,点
,点![]() 为
为![]() 上的动点,且
上的动点,且![]() .
.
(1)求![]() 的长度;
的长度;
(2)在点D运动的过程中,弦AD的延长线交BC的延长线于点E,问ADAE的值是否变化?若不变,请求出ADAE的值;若变化,请说明理由.
(3)在点D的运动过程中,过A点作AH⊥BD,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=900,∠B=∠E=300.



(1)操作发现如图2,固定△ABC,使△DEC绕点C旋转。当点D恰好落在BC边上时,填空:线段DE与AC的位置关系是 ;
② 设△BDC的面积为S1,△AEC的面积为S2。则S1与S2的数量关系是 。
(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想。
(3)拓展探究
已知∠ABC=600,点D是其角平分线上一点,BD=CD=4,OE∥AB交BC于点E(如图4),若在射线BA上存在点F,使S△DCF =S△BDC,请直接写出相应的BF的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了弘扬我国古代数学发展的伟大成就,某校九年级进行了一次数学知识竞赛,并设立了以我国古代数学家名字命名的四个奖项:“祖冲之奖”、“刘徽奖”、“赵爽奖”和“杨辉奖”,根据获奖情况绘制成如图1和图2所示的条形统计图和扇形统计图,并得到了获“祖冲之奖”的学生成绩统计表:
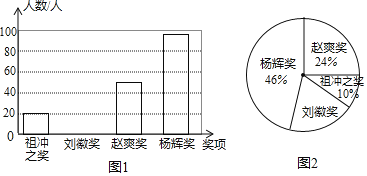
“祖冲之奖”的学生成绩统计表:
分数 | 80 | 85 | 90 | 95 |
人数 | 4 | 2 | 10 | 4 |
根据图表中的信息,解答下列问题:
![]() 这次获得“刘徽奖”的人数是多少,并将条形统计图补充完整;
这次获得“刘徽奖”的人数是多少,并将条形统计图补充完整;
![]() 获得“祖冲之奖”的学生成绩的中位数是多少分,众数是多少分;
获得“祖冲之奖”的学生成绩的中位数是多少分,众数是多少分;
![]() 在这次数学知识竟赛中有这样一道题:一个不透明的盒子里有完全相同的三个小球,球上分别标有数字“
在这次数学知识竟赛中有这样一道题:一个不透明的盒子里有完全相同的三个小球,球上分别标有数字“![]() ”,“
”,“![]() ”和“2”,随机摸出一个小球,把小球上的数字记为x放回后再随机摸出一个小球,把小球上的数字记为y,把x作为横坐标,把y作为纵坐标,记作点
”和“2”,随机摸出一个小球,把小球上的数字记为x放回后再随机摸出一个小球,把小球上的数字记为y,把x作为横坐标,把y作为纵坐标,记作点![]() 用列表法或树状图法求这个点在第二象限的概率.
用列表法或树状图法求这个点在第二象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
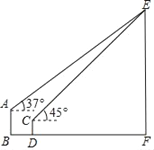
【题目】如图,甲楼AB高20m,乙楼CD高10m,两栋楼之间的水平距离BD=20m,为了测量某电视塔EF的高度,小明在甲楼楼顶A处观测电视塔塔顶E,测得仰角为37°,小丽在乙楼楼顶C处观测电视塔塔顶E,测得仰角为45°,求电视塔的高度EF.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,![]() ≈1.4,结果保留整数)
≈1.4,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:小明研究了这样一个问题:求使得等式![]() 成立的x的个数.小明发现,先将该等式转化为
成立的x的个数.小明发现,先将该等式转化为![]() ,再通过研究函数
,再通过研究函数![]() 的图象与函数
的图象与函数![]() 的图象(如图)的交点,使问题得到解决.
的图象(如图)的交点,使问题得到解决.
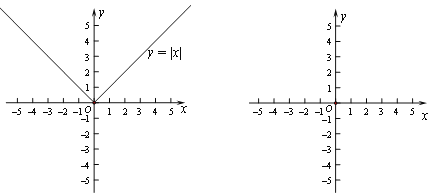
(1)当k=1时,使得原等式成立的x的个数为_______;
(2)当0<k<1时,使得原等式成立的x的个数为_______;
(3)当k>1时,使得原等式成立的x的个数为_______.
参考小明思考问题的方法,解决问题:关于x的不等式![]() 只有一个整数解,求
只有一个整数解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com