

���� ��1���ӳ�BA��P��ʹAP=CM����SAS�жϳ���CDM�ա�ADP���õ�DM=DP�����жϳ���MDN=��PDN���Ӷ���SAS�ó���DMN�ա�DPN�����ɣ�
��2���ӳ�BA��P��ʹAP=CM����SAS�жϳ���CDM�ա�ADP���õ�DM=DP�����жϳ���MDN=��PDN���Ӷ���SSS�ó���DMN�ա�DPN�����ɣ�
��3���������A�͡�EOF�ó���A+��EOF=180�㣬Ȼ���ã�1���Ľ���HG=HP=HF+FP������ֵHF=1200�ף�FP=1000�ף����ɣ�
��� �⣺��1����ͼ1��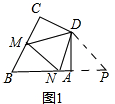
�ӳ�BA��P��ʹAP=CM������PD��
�ߡ�BAD=��C=90�㣬
���DAP=90�㣬
�ڡ�CDM�͡�ADP��$\left\{\begin{array}{l}{CM=AP}\\{��C=��DAP}\\{CD=AD}\end{array}\right.$��
���CDM�ա�ADP��SAS����
��DM=DP����CDM=��ADP��
���ı���ABCD�У���C=��BAD=90�㣬��B=60�㣬
������ı��ε��ڽǺ͵ã���ADC=120�㣬
�ߡ�MDN=60�㣬
���CDM+��ADN=60�㣬
�ߡ�CDM=��ADP��
���MDN=��PDN��
�ڡ�DMN�͡�DPN�У�$\left\{\begin{array}{l}{DM=DP}\\{��MDN=��PDN}\\{DN=DN}\end{array}\right.$��
���DMN�ա�DPN��SAS����
��MN=PN=AN+AP=AN+CM��
�ʴ�Ϊ��SAS��SAS��MN=AN+CM
��2����ͼ2��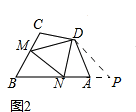
�ӳ�BA��P��ʹAP=CM������PD��
�ߡ�BAD+��C=180�㣬��BAD+��DAP=180�㣬
���C=��DAP��
�ڡ�CDM�͡�ADP��$\left\{\begin{array}{l}{CM=AP}\\{��C=��DAP}\\{CD=AD}\end{array}\right.$��
���CDM�ա�ADP��SAS����
��DM=DP����CDM=��ADP��
��CM=AP��
��MN=AN+CM=AN+AP=PN��
�ڡ�DMN�͡�DPN�У�$\left\{\begin{array}{l}{DM=DP}\\{MN=PN}\\{DN=DN}\end{array}\right.$
���DMN�ա�DPN��SSS����
���MDN=��PDN=��ADP+��ADN��
�ߡ�CDM=��ADP��
���MDN=��CDM+��ADN=$\frac{1}{2}$��ADC��
���ı���ABCD�У���BAD+��C=180�㣬
������ı��ε��ڽǺ͵ã���B+��ADC=180�㣬
���B+2��MDN=180�㣬
�ߡ�B=����
���MDN=$\frac{180��-��}{2}$=90��-$\frac{1}{2}$����
��3����ͼ3��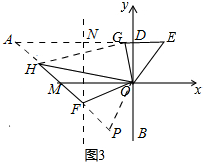
�ӳ�EG��FH����ڵ�A������F��FN��AE��
����ͬѧ��120��/���ӵ��ٶ���ƫ��60�㷽��ǰ����
���NFA=60�㣬
���A=30�㣬
��ͬѧ��ָ�Ӳ����������E������ͬѧ��ָ�Ӳ���ƫ��75���F����
���DOE=45�㣬��BOF=75�㣬
���MOF=90��-75��=15�㣬
���EOF=��DOE+��DOM+MOF=150�㣬
���A+��EOF=180�㣬
�ӳ�AF����P��ʹFP=GE��
���㣨1��������������HG=HP=HF+FP��
��ͬѧ��100��/���ӵ��ٶ�����������ǰ������ͬѧ��120��/���ӵ��ٶ���ƫ��60�㷽��ǰ����10���Ӻ�ָ�Ӳ����ס�����ͬѧ�ֱ�G��H����
��GE=100��10=1000�ף�HF=120��10=1200�ף�
��HG=HF+FP=1200+1000=2200�ף�
�����ס�����ͬѧ֮��ľ���Ϊ2200�ף�
���� �������ı����ۺ��⣬��Ҫ�������ڲ��ǣ�ȫ�������ε����ʺ��ж�����λ�ǣ����۵�Ӧ�ã�����ȫ���������ǽⱾ��Ĺؼ������ý�����ס�����ͬѧ֮��ľ����ǽⱾ����ѵ㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��-3�� | B�� | ��0��3�� | C�� | ��-3��0�� | D�� | ��-$\frac{9}{2}$��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
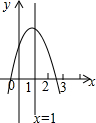 ���κ���y=ax2+bx+c��a��b�dz�����a��0��ͼ��ĶԳ�����ֱ��x=1����Ľ�������һ����-1��0֮�䣬��һ��������2��3֮�䣬��ͼ��ʾ����������˵������ab��0����a-b+c��0����3a+c��0���ܵ�-1��x��3ʱ��y��0��������ȷ�ĸ����� ��������
���κ���y=ax2+bx+c��a��b�dz�����a��0��ͼ��ĶԳ�����ֱ��x=1����Ľ�������һ����-1��0֮�䣬��һ��������2��3֮�䣬��ͼ��ʾ����������˵������ab��0����a-b+c��0����3a+c��0���ܵ�-1��x��3ʱ��y��0��������ȷ�ĸ����� ��������| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{8}$ | B�� | $\sqrt{\frac{1}{2}}$ | C�� | $\sqrt{12}$ | D�� | $\sqrt{18}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{x}$ | B�� | $\sqrt{{x}^{2}+1}$ | C�� | $\sqrt{{x^2}-2}$ | D�� | $\root{3}{27}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | $\frac{1}{2}$ | C�� | 2 | D�� | $-\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$ | B�� | -$\sqrt{2}$ | C�� | $\frac{\sqrt{2}}{2}$ | D�� | -$\frac{\sqrt{2}}{2}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com