
【题目】如图,△ABD内接于⊙O,AB为⊙O的直径,C为弧AD的中点,CH⊥AB于点E,交AD于点P,交⊙O于点H,连接DH,连接BC交AD于点F.下列结论中:①DH⊥CB;②CP=PF;③CH=AD;④APAD=CFCB;⑤若⊙O的半径为5,AF=![]() ,则CH=
,则CH=![]() .正确的有( )
.正确的有( )

A.2个B.3个C.4个D.5个
【答案】C
【解析】
根据已知条件得到∠H=∠ABC,∠C+∠ABC=90°,于是得到∠H+∠C=90°,求得DH⊥BC,故①正确;根据![]() ,得到∠CBD=∠ABC,根据圆周角定理得到∠ADB=90°,求得∠BFD+∠DBF=90°,得到∠C=∠CFP,于是求得CP=PF,故②正确;根据垂径定理得到
,得到∠CBD=∠ABC,根据圆周角定理得到∠ADB=90°,求得∠BFD+∠DBF=90°,得到∠C=∠CFP,于是求得CP=PF,故②正确;根据垂径定理得到![]() ,求得
,求得![]() ,于是得到CH=AD;故③正确;连接AC,BH,得到∠ACH=∠CAD,求得AP=CP,根据垂径定理得到
,于是得到CH=AD;故③正确;连接AC,BH,得到∠ACH=∠CAD,求得AP=CP,根据垂径定理得到![]() ,求得BC=BH,根据相似三角形的性质即可得到结论.
,求得BC=BH,根据相似三角形的性质即可得到结论.
解:∵C为弧AD的中点,
∴![]()
∴∠H=∠ABC,
∵CH⊥AB,
∴∠C+∠ABC=90°,
∴∠H+∠C=90°,
∴DH⊥BC,故①正确;
∵![]() ,
,
∴∠CBD=∠ABC,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠BFD+∠DBF=90°,
∴∠C=∠BFD,
∵∠CFP=∠DFB,
∴∠C=∠CFP,
∴CP=PF,故②正确;
∵AB为⊙O的直径,C为弧AD的中点,CH⊥AB,
∴![]() ,
,
∴![]() ,
,
∴CH=AD;故③正确;
连接AC,BH,
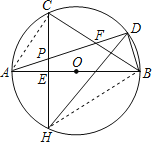
则∠ACH=∠CAD,
∴AP=CP,
∵CH⊥AB,
∴![]() ,
,
∴BC=BH,
∴∠BCH=∠BHC,
∴∠CFP=∠BHC,
∵∠PCF=∠BCH,
∴△CPF∽△CBH,
∴![]() ,
,
∴PCCH=CFCB,
∵PC=AP,CH=AD,
∴APAD=CFCB,故④正确;
∵∠CAF=∠ABC,
又∵∠ACF=∠BCA,
∴△CAF∽△CBA,
∴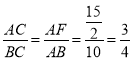 ,
,
又∵AB=10,
∴AC=6,BC=8.
根据直角三角形的面积公式,得:ACBC=ABCE,
∴6×8=10CE.
∴CE=![]()
又∵CH=HE,
∴CH=2CE=![]() .故⑤错误,
.故⑤错误,
故选:C.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
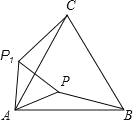
【题目】△ABC 是等边三角形,点 P 在△ABC 内,PA=2,将△PAB 绕点 A 逆时针旋转得到△P1AC,则 P1P 的长等于( )
A. 2 B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
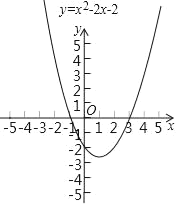
【题目】在实际问题中往往需要求得方程的近似解,这个时候,我们通常利用函数的图象来完成.如,求方程x2﹣2x﹣2=0的实数根的近似解,观察函数y=x2﹣2x﹣2的图象,发现,当自变量为2时,函数值小于0(点(2,﹣2)在x轴下方),当自变量为3时,函数值大于0(点(3,1)在x轴上方).因为抛物线y=x2﹣2x﹣2是一条连续不断的曲线,所以抛物线y=x2﹣2x﹣2在2<x<3这一段经过x轴,也就是说,当x取2、3之间的某个值时,函数值为0,即方程x2﹣2x﹣2=0在2、3之间有根.进一步,我们取2和3的平均数2.5,计算可知,对应的数值为﹣0.75,与自变量为3的函数值异号,所以这个根在2.5与3之间任意一个数作为近似解,该近似解与真实值的差都不会大于3﹣2.5=0.5.重复以上操作,随着操作次数增加,根的近似值越来越接近真实值.用以上方法求得方程x2﹣2x﹣2=0的小于0的解,并且使得所求的近似解与真实值的差不超过0.3,该近似解为_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,网格中每个小正方形的边长为1,点A,B均在格点上.则线段AB的长为 .请借助网格,仅用无刻度的直尺在AB上作出点P,使AP=![]() .
.
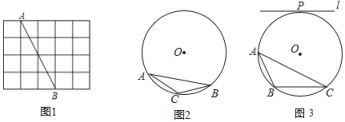
(2)⊙O为△ABC的外接圆,请仅用无刻度的直尺,依下列条件分别在图2,图3的圆中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法,请下结论注明你所画的弦).
①如图2,AC=BC;
②如图3,P为圆上一点,直线l⊥OP且l∥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别是A(-3,2),B(-1,4),C(0,2).
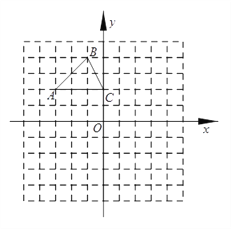
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;
(2)平移△ABC,若A的对应点A2的坐标为(-5,-2),画出平移后的△A2B2C2;
(3)若将△A2B2C2绕某一点旋转可以得到△A1B1C,请直接写出旋转中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(12,0),B(8,6),C(0,6).动点P从点O出发,以每秒3个单位长度的速度沿边向OA终点A运动;动点Q从点B同时出发,以每秒2个单位长度的速度沿边BC向终点C运动.设运动的时间为t秒,PQ![]() =y.
=y.
(1)直接写出y关于t的函数解析式及t的取值范围: ;
(2)当PQ=3![]() 时,求t的值;
时,求t的值;
(3)连接OB交PQ于点D,若双曲线![]() 经过点D,问k的值是否变化?若不变化,请求出k的值;若变化,请说明理由.
经过点D,问k的值是否变化?若不变化,请求出k的值;若变化,请说明理由.
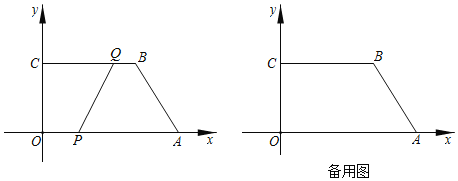
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接疫情彻底结束后的购物高峰,某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:
运动鞋价格 | 甲 | 乙 |
进价(元/双) | m | m﹣20 |
售价(元/双) | 240 | 160 |
已知:用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.
(1)求m的值;
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)不少于21700元,且甲种运动鞋的数量不超过100双,问该专卖店共有几种进货方案?
(3)在(2)的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠a(50<a<70)元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 与一次函数
与一次函数![]() 的图象交于两点A(1,3)、B(n,-1).
的图象交于两点A(1,3)、B(n,-1).
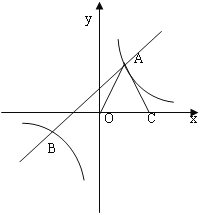
(1)求这两个函数的解析式;
(2)观察图象,请直接写出不等式![]() 的解集;
的解集;
(3)点C为x轴正半轴上一点,连接AO、AC,且AO=AC,求⊿AOC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com