练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．已知|x|=3，y2=16，xy＜0，则x-y=（　　）
    A．-7或-1B．7或1C．1或-1D．7或-7

    分析 先求出x，y的值即可得出结论．

    解答 解：因为|x|=3，所以x=±3．
    因为y2=16，所以y=±4．
    又因为xy＜0，所以x、y异号，
    当x=3时，y=-4，所以x-y=7；
    当x=-3时，y=4，所以x-y=-7
    故选D．

    点评 本题是绝对值、平方根和有理数减法的综合试题，同时本题还渗透了分类讨论的数学思想．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

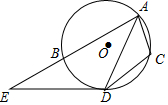    16．如图，已知AD是⊙O的弦，$\widehat{BD}$=$\widehat{CD}$，DE是⊙O的切线且与弦AB的延长线相交于点E，若AC=3，AE=8，则AD的长为2$\sqrt{6}$．

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年江苏省苏州太仓市第二学期初一期中模拟数学试卷（解析版） 题型：单选题

    氢原子中电子和原子核之间的距离为0.00000000529厘米，用科学记数法表示这个距离为( )

    A. 5.29×10－8 cm ； B. 5.29×10－9cm； C. 0.529×10－8 cm； D. 52.9×10－10 cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．如果一个几何体从三个方向看到的图形之一是长方形，这个几何体可能是长方体．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．△ABD中，DA=DB，C为BD延长线上一点，BE⊥AC于点E，作∠ADB的角平分线DF交BE于点F，连接AF．
    （1）如图1，求证：∠FAB=∠FBA；
    （2）如图2，若∠ADB=90°，点G与点D关于直线AC对称，连接AG，判断∠GAC与∠EAF的数量关系，并证明你的结论．
    （3）如图3，在（2）的条件下，若AE=2，DG=6，求AB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．【探究证明】：
    （1）某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究，提出下列问题，请你给出证明．
    如图1，矩形ABCD中，EF⊥GH，EF分别交AB，CD于点E，F，GH分别交AD，BC于点G，H．求证：$\frac{EF}{GH}$=$\frac{AD}{AB}$；
    【结论应用】：
    （2）如图2，在满足（1）的条件下，又AM⊥BN，点M，N分别在边BC，CD上，若$\frac{EF}{GH}$=$\frac{8}{11}$，则$\frac{BN}{AM}$的值为$\frac{8}{11}$；
    【联系拓展】：
    （3）如图3，四边形ABCD中，∠ABC=90°，AB=AD=10，BC=CD=5，AM⊥DN，点M，N分别在边BC，AB上，则$\frac{DN}{AM}$=$\frac{4}{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

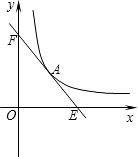    8．如图，已知A（m，2）是直线l与双曲线y=$\frac{3}{x}$的交点．
    （1）求m的值．
    （2）若直线l分别与x轴、y轴交于E、F两点，并且A为EF的中点，试确定l的解析式．
    （3）在双曲线上另取一点B，作BK⊥x轴于K，将（2）中的直线l绕点A旋转后所得的直线记为l′，若l′与y轴的正半轴交于点C，且OC=$\frac{1}{4}$OF，试问，在y轴上是否存在点P，使得S△PCA=S△BOK？若存在，求出P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图1，△ABC中，AC=AB，以AB为直径的⊙O分别交直线AC、BC于D、E两点．
    （1）如图2，若∠C=60°，求证：AD=BE；
    （2）如图3，过点A作AF平行BC，交⊙O于点F，点G为AF上一点，连接OG、OF，若∠GOF=90°-$\frac{3}{2}$∠ABC，求证：AC=2AG；
    （3）在（2）的条件下，在AB的延长线上取点M，连接GM，使∠M=2∠GOF，若AD：CD=1：3，BC=2$\sqrt{6}$，求BM的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

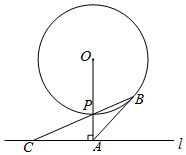    6．如图，已知直线l与⊙O相离，OA⊥l于点A，OA=5，OA与⊙O相交于点P，点B在⊙O上，BP的延长线交直线l于点C，连结AB，AB=AC．
    （1）直线AB与⊙O相切吗？请说明理由；
    （2）线段BC的中点为M，当⊙O的半径r为多少时，直线AM与⊙O相切．

    查看答案和解析>>

    同步练习册答案