
【题目】已知△ABC是边长为4的等边三角形,BC在x轴上,点D为BC的中点,点A在第一象限内,AB与y轴的正半轴交与点E,已知点B(﹣1,0).
(1)点A的坐标: , 点E的坐标:;
(2)若二次函数y=﹣ ![]() x2+bx+c过点A、E,求此二次函数的解析式;
x2+bx+c过点A、E,求此二次函数的解析式;
(3)P是AC上的一个动点(P与点A、C不重合)连结PB、PD,设l是△PBD的周长,当l取最小值时,求点P的坐标及l的最小值并判断此时点P是否在(2)中所求的抛物线上,请充分说明你的判断理由.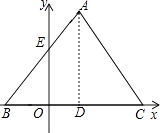
【答案】
(1)(1,2 ![]() );(0,
);(0, ![]() )
)
(2)
解:因为抛物线y=﹣ ![]() x2+bx+c过点A、E,
x2+bx+c过点A、E,
由待定系数法得:c= ![]() ,b=
,b= ![]() ,
,
抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]()
(3)
解:作点D关于AC的对称点D',
连接BD'交AC于点P,则PB与PD的和取最小值,
即△PBD的周长L取最小值,如图2
 .
.
∵D、D′关于直线AC对称,
∴DD′⊥AC,即∠D′DC=30°,
DF= ![]() ,DD'=2
,DD'=2 ![]() ,
,
求得点D'的坐标为(4, ![]() ),
),
直线BD'的解析式为:y= ![]() x+
x+ ![]() ,
,
直线AC的解析式为:y=﹣ ![]() x+3
x+3 ![]() ,
,
求直线BD'与AC的交点可,得
点P的坐标( ![]() ,
, ![]() ).
).
此时BD'= ![]() =
= ![]() =2
=2 ![]() ,
,
所以△PBD的最小周长L为2 ![]() +2,
+2,
把点P的坐标代入y=﹣ ![]() +
+ ![]() x+
x+ ![]() 成立,
成立,
所以此时点P在抛物线上.
【解析】解:(1)连接AD,如图1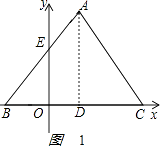 ,
,
∵△ABC是边长为4的等边三角形,又B的坐标为(﹣1,0),BC在x轴上,A在第一象限,
∴点C在x轴的正半轴上,
∴C的坐标为(3,0),由中点坐标公式,得:D的坐标为(1,0).
显然AD⊥BC且AD= ![]() BD=2
BD=2 ![]() ,
,
∴A的坐标是(1,2 ![]() ).
).
OE= ![]() AD,得E(0,
AD,得E(0, ![]() );
);
(1)△ABC是边长为4的等边三角形,则BC=4,而点D为BC的中点,BD=2,点B(﹣1,0),则OD=1,就可以求出A的横坐标,等边三角形的高线长,就是A的纵坐标.在直角三角形OBE中,根据三角函数可以求出OE的长,即得到E点的纵坐标.(2)已经求出A,E的坐标,根据待定系数法就可以求出函数的解析式.(3)先作点D关于AC的对称点D',连接BD'交AC于点P,则PB与PD的和取最小值,即△PBD的周长L取最小值.根据三角函数求的D′的坐标,再求出直线BD′的解析式,以及直线AC的解析式,两直线的交点就是P的坐标.把点P的坐标代入二次函数的解析式,就可以判断是否在函数的图象上.


科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+8与x轴、y轴分别交于A.B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则点M的坐标是( )
x+8与x轴、y轴分别交于A.B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则点M的坐标是( )

A. (0,4) B. (0,3) C. (﹣4,0) D. (0,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
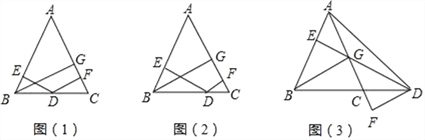
【题目】如图,在△ABC中,AB=AC,BG⊥AC于G,DE⊥AB于E,DF⊥AC于F.
(1)在图(1)中,D是BC边上的中点,判断DE+DF和BG的关系,并说明理由.
(2)在图(2)中,D是线段BC上的任意一点,DE+DF和BG的关系是否仍然成立?如果成立,证明你的结论;如果不成立,请说明理由.
(3)在图(3)中,D是线段BC延长线上的点,探究DE、DF与BG的关系.(不要求证明,直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题.
大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,但是由于1<
的小数部分我们不可能全部地写出来,但是由于1<![]() <2,所以
<2,所以![]() 的整数部分为1,将
的整数部分为1,将![]() 减去其整数部分1,差就是小数部分
减去其整数部分1,差就是小数部分![]() -1,根据以上的内容,解答下面的问题:
-1,根据以上的内容,解答下面的问题:
(1)![]() 的整数部分是 ,小数部分是 ;
的整数部分是 ,小数部分是 ;
(2)1+![]() 的整数部分是 ,小数部分是 ;
的整数部分是 ,小数部分是 ;
(3)若设2+![]() 整数部分是x,小数部分是y,求x-y的值.
整数部分是x,小数部分是y,求x-y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( ) 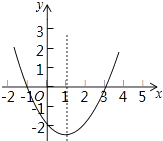
A.函数有最小值
B.当﹣1<x<3时,y>0
C.当x<1时,y随x的增大而减小
D.对称轴是直线x=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣4x与x轴交于点O,A,顶点为B,连接AB并延长,交y轴于点C,则图中阴影部分的面积和为( ) 
A.4
B.8
C.16
D.32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】著名的瑞士数学家欧拉曾指出:可以表示为四个整数平方之和的甲、乙两数相乘,其乘积仍然可以表示为四个整数平方之和,即![]()
![]() ,这就是著名的欧拉恒等式,有人称这样的数为“不变心的数”.实际上,上述结论可减弱为:可以表示为两个整数平方之和的甲、乙两数相乘,其乘积仍然可以表示为两个整数平方之和.
,这就是著名的欧拉恒等式,有人称这样的数为“不变心的数”.实际上,上述结论可减弱为:可以表示为两个整数平方之和的甲、乙两数相乘,其乘积仍然可以表示为两个整数平方之和.
【动手一试】
试将![]() 改成两个整数平方之和的形式.
改成两个整数平方之和的形式. ![]() ;
;
【阅读思考】
在数学思想中,有种解题技巧称之为“无中生有”.例如问题:将代数式![]() 改成两个平方之差的形式.解:原式
改成两个平方之差的形式.解:原式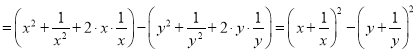 ﹒
﹒
【解决问题】
请你灵活运用利用上述思想来解决“不变心的数”问题:将代数式![]() 改成两个整数平方之和的形式(其中a、b、c、d均为整数),并给出详细的推导过程﹒
改成两个整数平方之和的形式(其中a、b、c、d均为整数),并给出详细的推导过程﹒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,己知O为坐标原点,点A(3,0),B(0,4),以点A为旋转中心,把△ABO顺时针旋转,得△ACD.记旋转角为α.∠ABO为β.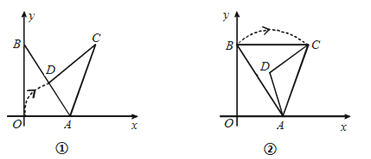
(Ⅰ)如图①,当旋转后点D恰好落在AB边上时,求点D的坐标;
(Ⅱ)如图②,当旋转后满足BC∥x轴时,求α与β之间的数量关系:
(Ⅲ)当旋转后满足∠AOD=β时,求直线CD的解析式(直接写出结果即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com