
 ���ֲ�����
���ֲ��������� ��1�����ü������Ի�����Ӧ��ͼ�Σ�
��2����������������������BAD�͡�ADB������ж�������ȣ�
��������������������BCD�͡�BDC������ж�������ȣ�
�����ò�������á�ADCΪֱ�������Σ���DAC+��BCD=90��ȣ�
��� �⣺��1����ͼ��BC��BDΪ������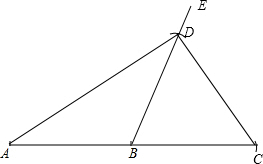
��2���١�BAD=32�㣬��ADB=32�㣬���BAD=��ADB��
�ڡ�BCD=58�㣬��BDC=58�㣬���ԡ�BCD=��BDC��
�ۡ�ADCΪֱ�������Σ���DAC+��BCD=90�㣮
���� ���⿼������ͼ-������ͼ��������ͼ�������ֻ�����ͼ�Ļ����Ͻ�����ͼ��һ���ǽ���˼���ͼ�ε����ʺͻ�����ͼ���������������Ŀ�Ĺؼ�����Ϥ��������ͼ�ε����ʣ���ϼ���ͼ�εĻ������ʰѸ�����ͼ���ɻ�����ͼ��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{3}{4}$ | D�� | .1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{a+b}{ab}$ | B�� | $\frac{ab}{2��a+b��}$ | C�� | $\frac{a+b}{2ab}$ | D�� | $\frac{ab}{a+b}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
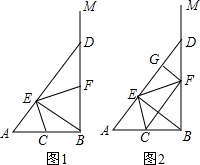 ��ͼ����ABMΪֱ�ǣ���CΪ�߶�BA���е㣬��D������BM�ϵ�һ�����㣨�����B�غϣ�������AD����BE��AD������ΪE������CE������E��EF��CE����BD��F��
��ͼ����ABMΪֱ�ǣ���CΪ�߶�BA���е㣬��D������BM�ϵ�һ�����㣨�����B�غϣ�������AD����BE��AD������ΪE������CE������E��EF��CE����BD��F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��m+n����-m+n�� | B�� | ��x3-y3����x3+y3�� | C�� | ��-a-b����a+b�� | D�� | �� $\frac{1}{3}$a-b���� $\frac{1}{3}$a+b�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com