
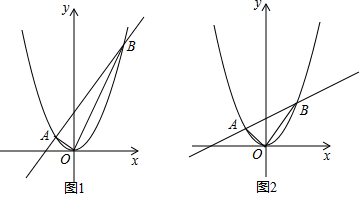
���� ��1���ֱ���x=0�����y��ֵ���ɽ�����⣮
��2���ٷ���һ�����ù��ɶ������涨���жϣ��������������������ε������жϣ�����������ֱ�������ε��ж������ж���
��֤���������Ƣ�
��3������S��AOB=$\frac{1}{2}$��4����|x1|+|x2|�����������κ��������ö��κ��������ʼ��ɽ�����⣮
��� �⣺��1����������y��Ľ������꣨0��0����ֱ����y��Ľ������꣨0��4����
��2���ٵ�m=$\frac{3}{2}$ʱ��ֱ��Ϊy=$\frac{3}{2}$x+4��
��$\left\{\begin{array}{l}y=\frac{1}{4}{x^2}\\ y=\frac{3}{2}x+4\end{array}\right.$�����$\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$��$\left\{\begin{array}{l}{x=8}\\{y=16}\end{array}\right.$��
��������ͼ��Ľ���ΪA��-2��1����B��8��16����
�ֱ�����A�͵�B��x��Ĵ��߶�AM��BN����M��-2��0����N��8��0����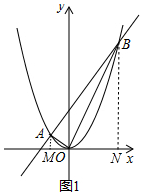
����һ�������ɶ����涨����
��AB2=��8+2��2+16-1��2=325��AO2=5��BO2=320��
��AO2+BO2=325=AB2��
���AOB��ֱ�������Σ�
��������������������
��AM•BN=OM•ON=16��
��$\frac{AM}{ON}=\frac{OM}{BN}$��
��Rt��OAM��Rt��BON��
���AOM=��OBN��
�ߡ�BON+��OBN=90��
���AOM+BON=90�㣬
���AOB=90�㣬
���AOB��ֱ�������Σ�
����������ֱ���������ж���
��A��B���е�ΪC����C��3��8.5��
��OC=$\sqrt{{3}^{2}+8��{5}^{2}}$=$\frac{1}{2}$$\sqrt{325}$=$\frac{1}{2}$AB��
���AOB��ֱ�������Σ�
�ڷ���һ����A��x1��y1����B��x2��y2����������$y=\frac{1}{4}{x^2}$��ֱ��y=mx+4�Ľ��㣬
���ԣ�x1��y1������x2��y2���Ƿ�����$\left\{\begin{array}{l}y=\frac{1}{4}{x^2}\\ y=mx+4\end{array}\right.$�������⣬
Ҳ����˵��x1��x2�Ƿ���$\frac{1}{4}$x2=mx+4������ʵ���⣬
���÷��̸�дΪx2-4mx-16=0������x1+x2=4m��x1x2=-16��
�ɢٵĽ�����̣����ǿ��Եõ���AB2=��x1-x2��2+��y1-y2��2��
��A��x1��y1����B��x2��y2����ֱ��y=mx+4�ϣ�
��y1=mx1+4��y2=mx2+4����y1-y2=m��x1-x2����
��AB2=��x1-x2��2+m2��x1-x2��2=��1+m2����x1-x2��2��
��x1+x2=4m��x1x2=-16��
�ࣨx1-x2��2=��x1+x2��2-4x1x2=16m2+64��
��AB2=��1+m2����16m2+64��=16��1+m2����m2+4����
ͬ���ģ�AO2=x12+y12=x12+��mx1+4��2=��1+m2��x12+8mx1+16��
BO2=��1+m2��x22+8mx2+16��
AO2+BO2=[��1+m2��x12+8mx1+16]+[��1+m2��x22+8mx2+16]
=��1+m2����x12+x22��+8m��x1+x2��+32��
��x12+x22=��x1+x2��2-2x1x2=16m2+32��
��AO2+BO2=��1+m2����16m2+32��+8m•4m+32=16��1+m2����m2+2��+32��m2+1��=16��1+m2��[��m2+2��+2]=16��1+m2����m2+4����AO2+BO2=16��1+m2����m2+4��=AB2��
���AOB��ֱ�������Σ�
��������x1+x2=4m��x1x2=-16
��y1y2=��mx1+4����mx2+4��=m2x1x2=4m��x1+x2��+16=m2��-16��+4m•4m+16=16��
��-x1x2=y1y2=16����AM•BN=OM•ON
��$\frac{AM}{ON}=\frac{OM}{BN}$��
��Rt��OAM��Rt��BON��
���AOM=��OBN��
�ߡ�BON+��OBN=90��
���AOM+BON=90�㣬
���AOB=90�㣬
���AOB��ֱ�������Σ�
����������A��B���е�ΪC����C[$\frac{1}{2}$��x1+x2����$\frac{1}{2}$��y1+y2��]����C��2m��2m2+4����
$OC=\sqrt{{{��2m��}^2}+{{��2{m^2}+4��}^2}}=2\sqrt{��{m^2}+1����{m^2}+4��}=\frac{1}{2}AB$��
���AOB��ֱ�������Σ�
��3����S��AOB=$\frac{1}{2}$��4����|x1|+|x2|��=2$\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$=2$\sqrt{16{m}^{2}+64}$��
�൱m=0ʱ����AOB�������Сֵ=16��
���� ���⿼����κ����ۺ��⡢һ�κ�����Ӧ�á����ɶ����Լ����ɶ������涨����ֱ�������ε��ж������ʡ����������ε��ж������ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ������ֱ�������ε������ж�������ѧ�����ò���������⣬ѧ�ṹ�����κ��������ֵ���⣬�����п�ѹ���⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
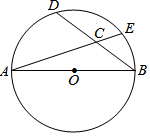 ��ͼ��AB�ǡ�O��ֱ������D�ǻ�AE���е㣬AB=5��BD=4����sin��ECB=$\frac{4}{5}$��
��ͼ��AB�ǡ�O��ֱ������D�ǻ�AE���е㣬AB=5��BD=4����sin��ECB=$\frac{4}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x-1��2=6 | B�� | ��x+1��2=6 | C�� | ��x+1��2=4 | D�� | ��x-1��2=1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
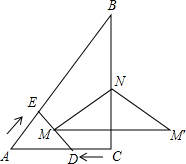 ��ͼ����ABC�У���C=90�㣬AC=3��BC=4����D��C�����������CA��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ��E��A�������AB��ÿ��1����λ���ȵ��ٶ���B�������˶�������E����B��ʱD��E��ֹͣ�˶�����M��DE���е㣬ֱ��MN��DE��ֱ��BC�ڵ�N����M����M�����ֱ��BC�Գƣ���D��E���˶�ʱ��Ϊt���룩��
��ͼ����ABC�У���C=90�㣬AC=3��BC=4����D��C�����������CA��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ��E��A�������AB��ÿ��1����λ���ȵ��ٶ���B�������˶�������E����B��ʱD��E��ֹͣ�˶�����M��DE���е㣬ֱ��MN��DE��ֱ��BC�ڵ�N����M����M�����ֱ��BC�Գƣ���D��E���˶�ʱ��Ϊt���룩���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{25}$=��5 | B�� | $\sqrt{6}$��6��һ��ƽ���� | ||
| C�� | 8���������ǡ�2 | D�� | -32������ƽ������3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com