
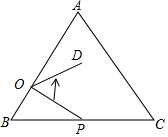
 在等边△ABC中,AC=9,点O在AB上,且BO=3,点P是BC上一动点,连结OP,将线段OP绕点O逆时针旋转60°得到线段OD,要使点D恰好落在AC边上,则BP的长是6.
在等边△ABC中,AC=9,点O在AB上,且BO=3,点P是BC上一动点,连结OP,将线段OP绕点O逆时针旋转60°得到线段OD,要使点D恰好落在AC边上,则BP的长是6. 分析 先利用旋转的性质得OP=OD,∠POD=60°,再根据平角的定义得到∠1+∠2=120°,接着根据等边三角形的性质得AB=AC=9,∠A=∠B=60°,所以∠2+∠3=120°,于是得到∠1=∠3,则可利用“AAS”判断△AOD≌△BPO,所以BP=AO=6.
解答 解:如图,
∵线段OP绕点O逆时针旋转60°得到线段OD,要使点D恰好落在AC边上,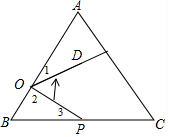
∴OP=OD,∠POD=60°,
∴∠1+∠2=120°,
∵△ABC为等边三角形,
∴AB=AC=9,∠A=∠B=60°,
∴∠2+∠3=120°,
∴∠1=∠3,
在△AOD和△BPO中
$\left\{\begin{array}{l}{∠A=∠B}\\{∠2=∠3}\\{PO=OD}\end{array}\right.$,
∴△AOD≌△BPO,
∴BP=AO,
而AO=AB-OB=9-3=6,
∴BP=6.
故答案为6.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的性质.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:解答题
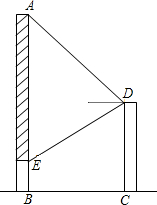 如图,为响应泰安市人民政府“形象重于生命”的号召,在甲建筑物上从A点到E点挂一长为30米的宣传条幅(如图),在乙建筑物的顶部D点测得条幅顶端A点的仰角为45°,测得条幅底端E点的俯角为30°,求底部不能直接到达的甲乙两建筑物之间的水平距离BC.
如图,为响应泰安市人民政府“形象重于生命”的号召,在甲建筑物上从A点到E点挂一长为30米的宣传条幅(如图),在乙建筑物的顶部D点测得条幅顶端A点的仰角为45°,测得条幅底端E点的俯角为30°,求底部不能直接到达的甲乙两建筑物之间的水平距离BC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
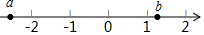 有理数a,b在数轴上的位置如图所示,则下列结论中,不正确的是( )
有理数a,b在数轴上的位置如图所示,则下列结论中,不正确的是( )| A. | a+b<0 | B. | a-b>0 | C. | $\frac{b}{a}$<0 | D. | |a|>|b| |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 求证:等腰三角形底边的中点到两腰的距离相等.
求证:等腰三角形底边的中点到两腰的距离相等. 证明:连接AD,
证明:连接AD,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式.例如图(1)可以用来解释(a+b)2-(a-b)2=4ab.那么通过图(2)面积的计算,验证了一个恒等式,此等式是( )
我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式.例如图(1)可以用来解释(a+b)2-(a-b)2=4ab.那么通过图(2)面积的计算,验证了一个恒等式,此等式是( )| A. | a2-b2=(a+b)(a-b) | B. | (a-b)2=a2-2ab+b2 | ||
| C. | (a+b)2=a2+2ab+b2 | D. | (a-b)(a+2b)=a2+ab-2b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com