
 如图,在△ABC中,AD平分∠BAC,过AD的中点O作EF⊥AD,分别交AB、AC于点E、F,连接DE、DF.
如图,在△ABC中,AD平分∠BAC,过AD的中点O作EF⊥AD,分别交AB、AC于点E、F,连接DE、DF.分析 (1)由于O是AD的中点,且EF⊥AD,所以AE=DE,AF=DF,由于AD平分∠BAC,所以∠EAO=∠FAO=90°,从易证AE=AF=DF=DE,所以四边形AEDF是菱形.
(2)由DE∥AC可知△BDE∽△BCA,从而可知$\frac{DE}{AC}=\frac{BD}{BC}$,代入数据即可求出AC的长度,从而可知CF的长度.
解答 (1)证明:∵O是AD的中点,且EF⊥AD,
∴AE=DE,AF=DF,
∵AD平分∠BAC,
∴∠EAO=∠FAO,
∵∠EOA=∠FOA=90°,
∴∠OEA=∠OFA,
∴AE=AF,
∴AE=AF=DF=DE,
∴四边形AEDF是菱形.
(2)∵四边形AEDF是菱形,
∴DE∥AC.
∴△BDE∽△BCA.
∴$\frac{DE}{AC}=\frac{BD}{BC}$,
∴$\frac{4}{AC}$=$\frac{8}{3+8}$
∴AC=$\frac{11}{2}$
∴CF=AC-CF=$\frac{3}{2}$
点评 本题考查相似三角形的综合问题,涉及相似三角形的性质,垂直平分线的判定,菱形的性质与判定,综合程度较高,属于中等题型.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:解答题
 绿色出行是对环境影响最小的出行方式,“共享单车”已成为北京的一道靓丽的风景线.某社会实践活动小组为了了解“共享单车”的使用情况,对本校教师在3月6日至3月10日使用单车的情况进行了问卷调查,以下是根据调查结果绘制的统计图的一部分:
绿色出行是对环境影响最小的出行方式,“共享单车”已成为北京的一道靓丽的风景线.某社会实践活动小组为了了解“共享单车”的使用情况,对本校教师在3月6日至3月10日使用单车的情况进行了问卷调查,以下是根据调查结果绘制的统计图的一部分: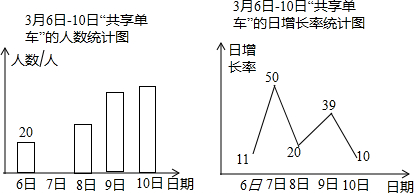
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=ax2+bx+c与x轴交于A(-1,0),B(4,0)与y轴交于点C(0,2),抛物线的对称轴交x轴于点D.
如图,抛物线y=ax2+bx+c与x轴交于A(-1,0),B(4,0)与y轴交于点C(0,2),抛物线的对称轴交x轴于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 种类 | 单价 |
| 米饭 | 0.5元/份 |
| A类套餐菜 | 3.5元/份 |
| B类套餐菜 | 2.5元/份 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD中,对角线AC、BD交于点O,且AC⊥BD,AC=BD,SABCD=8cm2,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的周长等于8cm.
如图,四边形ABCD中,对角线AC、BD交于点O,且AC⊥BD,AC=BD,SABCD=8cm2,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的周长等于8cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com