
| 3 |
| ||
| 3 |
| ||
| 3 |
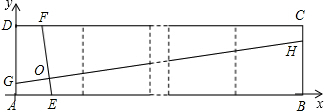
 解:分别过E、G两点作EM⊥CD,GN⊥BC,垂足分别为M、N,
解:分别过E、G两点作EM⊥CD,GN⊥BC,垂足分别为M、N,| EM |
| EF |
2
| ||
| 4 |
| ||
| 2 |
| 3 |
| ||
| 3 |
| 3 |
|
|
| ||
| 3 |
| ||
| 3 |


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:初中数学 来源:2012-2013学年江苏武进区九年级上第一次月考数学试卷(带解析) 题型:解答题
(1) 如图1,在正方形ABCD中,点E,F分别在边BC,CD上,AE,BF交于点O,∠AOF=90°.求证:BE=CF.
(2) 如图2,在正方形ABCD中,点E,H,F,G分别在边AB,BC,CD,DA上,EF,GH交于点O,∠FOH=90°, EF=4.求GH的长.
(3) 已知点E,H,F,G分别在矩形ABCD的边AB,BC,CD,DA上,EF,GH交于点O,∠FOH=90°,EF=4. 直接写出下列两题的答案:
①如图3,矩形ABCD由2个全等的正方形组成,求GH的长;
②如图4,矩形ABCD由n个全等的正方形组成,求GH的长(用n的代数式表示).
查看答案和解析>>
科目:初中数学 来源:2012年浙江省杭州市中考数学模拟试卷(46)(解析版) 题型:填空题
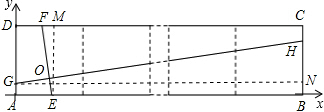
 的正方形并列组成,以AB、AD所在边的直线分别为x 轴、y轴建立直角坐标系.在矩形ABCD中,点E、H、F、G分别在边AB、BC、CD、DA上,EF、GH交于点O,∠FOH=90°,EF=4.当AG=1,则直线GH的解析式为 .
的正方形并列组成,以AB、AD所在边的直线分别为x 轴、y轴建立直角坐标系.在矩形ABCD中,点E、H、F、G分别在边AB、BC、CD、DA上,EF、GH交于点O,∠FOH=90°,EF=4.当AG=1,则直线GH的解析式为 .
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏武进区九年级上第一次月考数学试卷(解析版) 题型:解答题
(1) 如图1,在正方形ABCD中,点E,F分别在边BC,CD上,AE,BF交于点O,∠AOF=90°.求证:BE=CF.
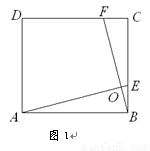
(2) 如图2,在正方形ABCD中,点E,H,F,G分别在边AB,BC,CD,DA上,EF,GH交于点O,∠FOH=90°, EF=4.求GH的长.
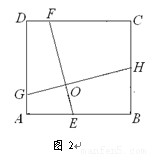
(3) 已知点E,H,F,G分别在矩形ABCD的边AB,BC,CD,DA上,EF,GH交于点O,∠FOH=90°,EF=4. 直接写出下列两题的答案:
①如图3,矩形ABCD由2个全等的正方形组成,求GH的长;

②如图4,矩形ABCD由n个全等的正方形组成,求GH的长(用n的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
(1) 如图,在正方形ABCD中,点E,F分别在边BC,CD上,AE,BF交于点O,∠AOF=90°.
求证:BE=CF.
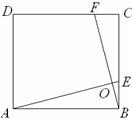
(2) 如图,在正方形ABCD中,点E,H,F,G分别在边AB,BC,CD,DA上,EF,GH交于点O,∠FOH=90°, EF=4.求GH的长.

(3) 已知点E,H,F,G分别在矩形ABCD的边AB,BC,CD,DA上,EF,GH交于点O,
∠FOH=90°,EF=4. 直接写出下列两题的答案:
①如图1,矩形ABCD由2个全等的正方形组成,求GH的长;
②如图2,矩形ABCD由n个全等的正方形组成,求GH的长(用n的代数式表示).

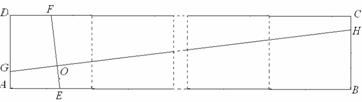
图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com