
(8分)如图,在长方形ABCD中,将△ABC沿AC对折至△AEC位置,CE与AD交于点F.

(1)试说明:AF=FC;
(2)如果AB=3,BC=4,求AF的长.
(1)详见解析;(2)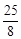 .
.
【解析】
试题分析:(1)观察图形,可得AE=DC,又∵∠FEA=∠DFC,∠AEF=∠CDF,由全等三角形判定方法证△AEF≌△CDF,即得EF=DF,从而得到AF=FC.(2)在Rt△CDF中应用勾股定理即可得.
试题解析:(1)证明:由矩形性质可知,AE=AB=DC,
根据对顶角相等得,∠EFA=∠DFC,
而∠E=∠D=90°,
∴由AAS可得,△AEF≌△CDF。∴AF=FC.
(2)设FA=x,则FC=x,FD= 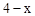 ,
,
在Rt△CDF中,CF2=CD2+DF2,即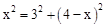 ,解得x=
,解得x=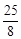 .
.
考点: 1.翻折变换(折叠问题);2.矩形的性质;3.全等三角形的判定与性质;4勾股定理.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:044
设边长为2a的正方形的中心A在直线l上,它的一组对边垂直于直线l,半径为r的⊙O的圆心O在直线l上运动,点A、O间距离为d.
(1)如图①,当r<a时,根据d与a、r之间关系,将⊙O与正方形的公共点个数填入下表:

所以,当r<a时,⊙O与正方形的公共点的个数可能有 个;
(2)如图②,当r=a时,根据d与a、r之间关系,将⊙O与正方形的公共点个数填入下表:

所以,当r=a时,⊙O与正方形的公共点个数可能有 个;
(3)如图③,当⊙O与正方形有5个公共点时,试说明r=![]() a;
a;

(4)就r>a的情形,请你仿照摰薄??保??I>O与正方形的公共点个数可能有
个數男问剑?辽俑?鲆桓龉赜趽⊙O与正方形的公共点个数數恼?方崧郏?ㄗⅲ旱冢?)小题若多给出一个正确结论,则可多得2分,但本大题得分总和不得超过12分)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
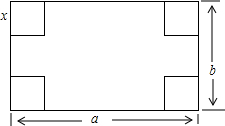 如图,在长和宽分别是a、b的长方纸片的四个角都剪去一个边长为x的正方形,当a=8,b=6,且剪去部分的面积等于剩余部分的面积的
如图,在长和宽分别是a、b的长方纸片的四个角都剪去一个边长为x的正方形,当a=8,b=6,且剪去部分的面积等于剩余部分的面积的 时,求正方形的边长x的值.
时,求正方形的边长x的值.查看答案和解析>>
科目:初中数学 来源:模拟题 题型:解答题

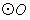 的半径为2,点A、B、C在
的半径为2,点A、B、C在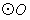 上,
上,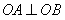 ,
,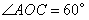 ,P是OB上一动点,求PA+PC的最小值;
,P是OB上一动点,求PA+PC的最小值;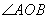 内一点,PO=8,Q,R分别是OA、OB上的动点,求
内一点,PO=8,Q,R分别是OA、OB上的动点,求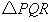 周长的最小值.
周长的最小值. 查看答案和解析>>
科目:初中数学 来源: 题型:
美化城市,改善人们的居住环境已成为城市建设的一项重要内容,近几年来,某
城市通过拆迁旧房,植草,栽树,使城市绿地面积不断增加.如图所示. (11分)
(1)
|
2004年底的绿地面积为 万平方
米,比2003年底增加了 万平方米,
在2002年,2003年,2004年这三年中,绿地
面积增加最多的是 年.
(2) ![]()
![]() 为满足城市发展需要,计划2005年绿地
为满足城市发展需要,计划2005年绿地
![]() 面积的增长率与2004年绿地面积的增
面积的增长率与2004年绿地面积的增
长率相同(增加的绿地面积包括植草面
积和栽树面积),其中植草面积是栽树面
积的3倍多3000平方米,已知栽树每平
方米需费用100元,植草每平方米需费用60元,问完成该计划需多少费用?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com