
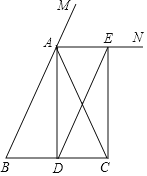
【题目】已知:如图,在△ABC中,AB=AC,AD是△ABC的中线,AN为△ABC的外角∠CAM的平分线,CE∥AD,交AN于点E.求证:四边形ADCE是矩形.
科目:初中数学 来源: 题型:
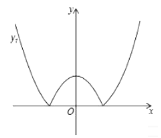
【题目】如图,将二次函数![]() (其中
(其中![]() )的图象在
)的图象在![]() 轴下方的部分沿
轴下方的部分沿![]() 轴翻折,图象的其余部分保持不变,形成新的图象记为
轴翻折,图象的其余部分保持不变,形成新的图象记为![]() ,另有一次函数
,另有一次函数![]() 的图象记为
的图象记为![]() ,若
,若![]() 与
与![]() 恰有两个交点时,则
恰有两个交点时,则![]() 的范围是________.
的范围是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
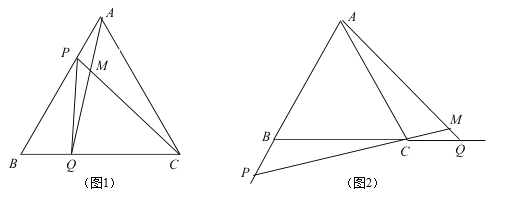
【题目】如图(1),点P、Q分别是边长为4cm的等边△ABC的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都是1cm/s
(1)设运动时间是t,则当t=__________s时,△PBQ是直角三角形.
(2)连接AQ、CP交于点M,则在P、Q运动的过程中,∠CMQ的大小变化吗?若变化,则说明理由,若不变,则求出它的度数;
(3)如图(2),若P,Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠CMQ的大小变化吗?若变化,则说明理由,若不变,则求出它的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
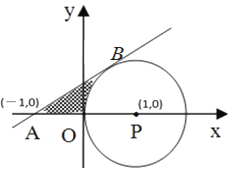
【题目】如图,在平面直角坐标系中,以(1,0)为圆心的⊙P与y轴相切于原点O,过点A(-1,0)的直线AB与⊙P相切于点B.
(1)求AB的长.
(2)求AB、OA与![]() 所围成的阴影部分面积.
所围成的阴影部分面积.
(3)求直线AB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
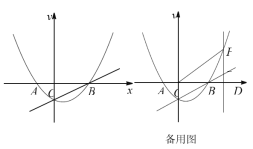
【题目】如图,抛物线![]() 的对称轴是直线
的对称轴是直线![]() ,与
,与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为抛物线上的一个动点,过点
为抛物线上的一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)求抛物线解析式;
(2)若点![]() 在第一象限内,当
在第一象限内,当![]() 时,求四边形
时,求四边形![]() 的面积;
的面积;
(3)将![]() 绕平面直角坐标系中某点逆时针旋转
绕平面直角坐标系中某点逆时针旋转![]() ,对应点为
,对应点为![]() ,
,![]() ,
,![]() ,当
,当![]() 中有两个顶点落在抛物线上时,直接写出
中有两个顶点落在抛物线上时,直接写出![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=26,P是AB上(不与点A、B重合)的任一点,点C、D为⊙O上的两点,若∠APD=∠BPC,则称∠CPD为直径AB的“回旋角”.
(1)若∠BPC=∠DPC=60°,则∠CPD是直径AB的“回旋角”吗?并说明理由;
(2)若![]() 的长为
的长为![]() π,求“回旋角”∠CPD的度数;
π,求“回旋角”∠CPD的度数;
(3)若直径AB的“回旋角”为120°,且△PCD的周长为24+13![]() ,直接写出AP的长.
,直接写出AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,其对称轴与抛物线交于点
,其对称轴与抛物线交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.

(1)求点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(2)点![]() 为抛物线对称轴上的一个动点,从点
为抛物线对称轴上的一个动点,从点![]() 出发,沿射线
出发,沿射线![]() 以每秒2个单位长度的速度运动,过点
以每秒2个单位长度的速度运动,过点![]() 作
作![]() 轴的平行线交抛物线于
轴的平行线交抛物线于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左边).设点
的左边).设点![]() 的运动时间为
的运动时间为![]() .
.
①当![]() 为何值时,以点
为何值时,以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形;
为顶点的四边形是平行四边形;
②连接![]() ,在点
,在点![]() 运动的过程中,是否存在点
运动的过程中,是否存在点![]() ,使得
,使得![]() ,若存在,求出点
,若存在,求出点![]() 的坐标:若不存在,请说明理由;
的坐标:若不存在,请说明理由;
③点![]() 在
在![]() 轴上,点
轴上,点![]() 为坐标平面内一点,以线段
为坐标平面内一点,以线段![]() 为对角线作菱形
为对角线作菱形![]() ,当
,当![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
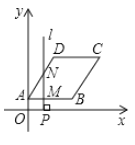
【题目】如图,在平面直角坐标私法中,四边形![]() 是菱形,
是菱形,![]() 轴,点
轴,点![]() 的坐标为
的坐标为![]() ,
,![]() ,垂直于
,垂直于![]() 轴的直线
轴的直线![]() 从
从![]() 轴出发,沿
轴出发,沿![]() 轴正方向以每秒1个单位长度的速度向右平移,设直线
轴正方向以每秒1个单位长度的速度向右平移,设直线![]() 与菱形
与菱形![]() 的两边分别交于点
的两边分别交于点![]() (点
(点![]() 在点
在点![]() 的上方),连接
的上方),连接![]() ,若
,若![]() 的面积为
的面积为![]() ,直线
,直线![]() 的运动时间为
的运动时间为![]() 秒(
秒(![]() ),则
),则![]() 与
与![]() 的函数图象大致是( )
的函数图象大致是( )
A.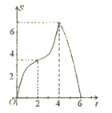 B.
B.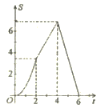 C.
C.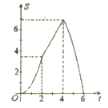 D.
D.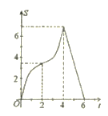
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com