练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在平面直角坐标系中，点A的坐标为（0，3），点B的坐标为（﹣2，0）．

    （1）把△ABO沿着x轴的正方向平移4个单位，请你画出平移后的△A′B′O′，其中A、B、O的对应点分别是A′、B′、O′（不必写画法）；

    （2）求△ABO平移前后所扫过的图形的面积S．


                  解：（1）

    ．

    （2）连接AA′、BB′，由平移的性质可知：AB∥A′B′，AB=A′B′，

    ∴四边形ABB′A′是平行四边形，

    ∵S=S四边形ABB'A′+S△A'B'O′，

    ∴，

    ∴△ABO平移前后所扫过的图形的面积为15平方单位．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    甲、乙两条轮船同时从港口A出发，甲轮船以每小时30海里的速度沿着北偏东60°的方向航行，乙轮船以每小时15海里的速度沿着正东方向行进，1小时后，甲船接到命令要与乙船会合，于是甲船改变了行进的速度，沿着东南方向航行，结果在小岛C处与乙船相遇．假设乙船的速度和航向保持不变，求：

    （1）港口A与小岛C之间的距离；

    （2）甲轮船后来的速度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在平面直角坐标系中，点A坐标为（1，3），将线段OA向左平移2个单位长度，得到线段O′A′，则点A的对应点A′的坐标为　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在直角坐标系中，把点A（﹣2，3）向上平移3个单位后得到点B，则点B的坐标是（　　）

    A．  （﹣2，6）    B．（﹣5，3）    C．（1，3）      D． （﹣2，0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，将等腰直角△ABC沿斜边BC方向平移得到△A1B1C1．若AB=3，若△ABC与△A1B1C1重叠部分面积为2，则BB1的长为　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


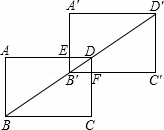
    如图，矩形ABCD中，AB=6cm，BC=8cm，将矩形沿着BD方向移动，设BB′=x．

    （1）当x为多少时，才能使平移后的矩形与原矩形重叠部分的面积为24cm2？

    （2）依次连接A′A，AC，CC′，C′A′，四边形ACC′A′可能是菱形吗？若可能，求出x的值；若不可能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在平面直角坐标系中，P点关于原点的对称点为P1（﹣3，﹣），P点关于x轴的对称点为P2（a，b），则=（　　）

    A．  ﹣2           B2 C．           4  D．           ﹣4

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    推理证明：如图1，在正方形ABCD和正方形CGFE中，连结DE、BG，设△DCE的面积为S1，△BCG的面积为S2，求证：S1=S2．

    猜想论证：如图2，将矩形ABCD绕点C按顺时针方向旋转后得到矩形FECG，连结DE、BG，设△DCE的面积为S1，△BCG的面积为S2，猜想S1、S2的数量关系，并加以证明．

    拓展探究：如图3，在△ABC中，AB=AC=10cm，∠B=30°，把△ABC沿AC翻折到△ACE，过点A作AD∥CE交BC于点D，在线段CE上存在点P，使△ABP的面积等于△ACD的面积，请你直接写出CP的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知矩形OABC的A点在x轴上，C点在y轴上，OC=6，OA=10．

    （1）在BC边上求作一点E，使OE=OA；（保留作图痕迹，不写画法）

    （2）求出点E的坐标．

    查看答案和解析>>

    同步练习册答案