
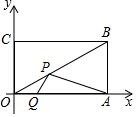
 已知在平面直角坐标系中,矩形OABC的顶点O为坐标原点,顶点A、B的坐标分别为(20,0),(20,10).P、Q分别为线段OB、OA上的动点,当PQ+PA最小时,点P的坐标为(12,6).
已知在平面直角坐标系中,矩形OABC的顶点O为坐标原点,顶点A、B的坐标分别为(20,0),(20,10).P、Q分别为线段OB、OA上的动点,当PQ+PA最小时,点P的坐标为(12,6). 分析 如图,作A关于OB的对称点A′,AA′交OB于H,作A′Q′⊥OA于Q′,A′Q′交OB于P′,此时P′A+P′Q′的值最小,求出P′的坐标即可解决问题.
解答 解:如图,作A关于OB的对称点A′,AA′交OB于H,作A′Q′⊥OA于Q′,A′Q′交OB于P′,此时P′A+P′Q′的值最小.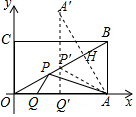
在Rt△OAB中,∵OA=20,AB=10,
∴OB=$\sqrt{A{B}^{2}+O{A}^{2}}$=10$\sqrt{5}$,
∵$\frac{1}{2}$•AB•OA=$\frac{1}{2}$•OB•AH,
∴AH=4$\sqrt{5}$,
∴AA′=2AH=8$\sqrt{5}$,
由△AA′Q′∽△BOA可得,$\frac{AQ′}{AB}$=$\frac{AA′}{OB}$,
∴$\frac{AQ′}{10}$=$\frac{8\sqrt{5}}{10\sqrt{5}}$,
∴AQ′=8,
∴OQ′=OA-AQ′=12,
∵tan∠BOA=$\frac{P′Q′}{OQ′}$=$\frac{AB}{OA}$,
∴$\frac{P′Q′}{10}$=$\frac{12}{20}$,
∴P′Q′=6,
∴P′(12,6).
∴当PQ+PA最小时,点P的坐标为(12,6)
点评 本题考查轴对称-最短问题、矩形的性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是学会利用的长解决最值问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
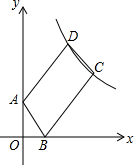 如图,A点坐标为(0,2),B点坐标为(1,0),点C是双曲线y=$\frac{k}{x}$(x>0)的上,将AB沿BC方向从B平移到C,点A的对应点为D,恰有AB=$\frac{1}{2}$BC,且点D也在双曲线上,则k的值等于12.
如图,A点坐标为(0,2),B点坐标为(1,0),点C是双曲线y=$\frac{k}{x}$(x>0)的上,将AB沿BC方向从B平移到C,点A的对应点为D,恰有AB=$\frac{1}{2}$BC,且点D也在双曲线上,则k的值等于12.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
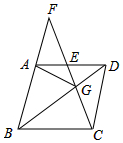 如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.
如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
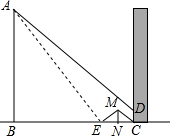 阳光明媚的一天,小华和小红两人想利用自己所学知识测量楼前旗杆的高度,某一时刻旗杆AB的影子一部分在地面上,另一部分在数学楼的墙面上高度记为CD,同一时刻小华蹲在地面N处,小华的影子刚好到达墙角C处;小红在小华与旗杆之间的直线BN上平放一平面镜,经过不断调整,直到小华能在镜子中看到旗杆的顶部,记平面镜的位置为E(忽略平面镜的高度),小华蹲着的高度记为MN(忽略眼晴到头顶的距离),且小华蹲在地面上的高度一直保持不变,此时小红测得BE=12.51米,EN=1.09米,NC=1.4米,CD=1米,求旗杆的高度.(结果精确到0.1米)
阳光明媚的一天,小华和小红两人想利用自己所学知识测量楼前旗杆的高度,某一时刻旗杆AB的影子一部分在地面上,另一部分在数学楼的墙面上高度记为CD,同一时刻小华蹲在地面N处,小华的影子刚好到达墙角C处;小红在小华与旗杆之间的直线BN上平放一平面镜,经过不断调整,直到小华能在镜子中看到旗杆的顶部,记平面镜的位置为E(忽略平面镜的高度),小华蹲着的高度记为MN(忽略眼晴到头顶的距离),且小华蹲在地面上的高度一直保持不变,此时小红测得BE=12.51米,EN=1.09米,NC=1.4米,CD=1米,求旗杆的高度.(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
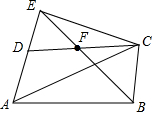 如图,在?ABCD中,∠ABC的平分线与AD的延长线交于点E,与CD交于点F,且点F是CD的中点,连结AC,CE.已知FC=3,FB=2$\sqrt{2}$,则△ACE的面积为4$\sqrt{14}$.
如图,在?ABCD中,∠ABC的平分线与AD的延长线交于点E,与CD交于点F,且点F是CD的中点,连结AC,CE.已知FC=3,FB=2$\sqrt{2}$,则△ACE的面积为4$\sqrt{14}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com