解:∵OC平分AB,
∴OH⊥AB,
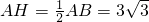
.
连接OA、OB,
设OA=r,则OH=r-3,
由勾股定理得
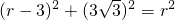
,
解得r=6.
∵OH⊥AB,OH=3,OA=6,
∴∠OAB=30度.
∵OA=OB,
∴∠OBA=30°,
∴∠AOB=120度.
∴
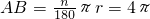
.
(2)作图如下图
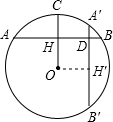
取A'B'中点H',连接OH',则OH'⊥A'B',H'是点H旋转后的对应点,
∴∠HOH'=90°,OH=OH'.
又OH⊥AB,
∴四边形HOH'D正方形.
∴HD=OH=3.
∴
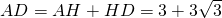
.
分析:(1)求弧长,需知道圆心角的度数,半径长.那么根据OC平分劣弧,可得到OH⊥AB,连接圆心和弦的端点构造直角三角形,利用三角函数求得半径和圆心角即可.
(2)旋转中心为O,旋转方向,顺时针,旋转角度90,分别得到A,B的对应点.利用旋转可得HD和OH的值相等,那么AD=AH+HD.
点评:求半径和圆心角通常是构造直角三角形利用特殊的三角函数来求解;做弦心距也是常用的辅助线方法.

 且交弦AB于点H,AB=
且交弦AB于点H,AB= ,CH=3.
,CH=3. 的长;(结果保留π)
的长;(结果保留π)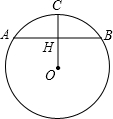
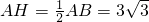 .
.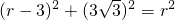 ,
,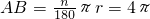 .
.
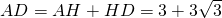 .
.

 =2,∠ADC=30°
=2,∠ADC=30°