
【题目】有这样一个问题:探究函数![]() 的图象与性质.下面是小文的探究过程,请补充完整:
的图象与性质.下面是小文的探究过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是__________;
的取值范围是__________;
(2)下表是![]() 与
与![]() 的几组对应值:
的几组对应值:

如图,在平面直角坐标系![]() 中,描出了以上表中各对应值为坐标的点.
中,描出了以上表中各对应值为坐标的点.
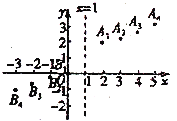
①观察图中各点的位置发现:点![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() 均关于某点中心对称,则该点的坐标为__________;
均关于某点中心对称,则该点的坐标为__________;
②小文分析函数![]() 表达式发现:当
表达式发现:当![]() 时,该函数的最大值为0,则该函数图象在直线
时,该函数的最大值为0,则该函数图象在直线![]() 左侧的最高点的坐标为__________;
左侧的最高点的坐标为__________;
(3)小文补充了该函数图象上两个点![]() ,
,![]() .
.
①在上图中描出这两个点,并画出该函数的图象;
②写出该函数的一条性质:__________.
【答案】(1)x≠1;(2)①(1,1);②(0,0);(3)①作图见解析;②当x<0时,y随x的增大而增大(答案不唯一).
【解析】
(1)分式的分母不等于零;
(2)①根据中心对称的性质和所对应的点点坐标即可求得,
②根据函数的性质求得即可;
(3)①根据坐标系中的点,用平滑的直线连接即可;
②可以从增减性、渐近性、连续性、与坐标轴交点、图象所在象限等方面作答.
解:(1)依题意得:2x-2≠0,
解得x≠1,
故答案是:x≠1;
(2)①点A1和B1,A2和B2,A3和B3,A4和B4均关于某点中心对称,B1(0,0),A1(2,2),
∴中心点点坐标为(1,1);
②∵当x<1时,该函数的最大值为0,
∴该函数图象在直线x=1左侧的最高点的坐标为(0,0);
故答案为(1,1);(0,0);
(3)①

②该函数的性质:
(ⅰ)当x<0时,y随x的增大而增大;
当0≤x<1时,y随x的增大而减小;
当1<x<2时,y随x的增大而减小;
当x≥2时,y随x的增大而增大.
(ⅱ)函数的图象经过第一、三、四象限.
(ⅲ)函数的图象与直线x=1无交点,图象由两部分组成.
故答案为当x<0时,y随x的增大而增大(答案不唯一);


科目:初中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中, ![]() ∥
∥![]() ,∠
,∠![]() =90°,
=90°,![]() =28cm,
=28cm, ![]() =24cm,
=24cm, ![]() =4cm,点
=4cm,点![]() 从点
从点![]() 出发,以1cm/s的速度向点
出发,以1cm/s的速度向点![]() 运动,点
运动,点![]() 从点
从点![]() 同时出发,以2cm/s的速度向点
同时出发,以2cm/s的速度向点![]() 运动,当其中一个动点到达端点停止运动时,另一个动点也随之停止运动。则四边
运动,当其中一个动点到达端点停止运动时,另一个动点也随之停止运动。则四边![]() 的面积
的面积![]() (cm2)与两动点运动的时间
(cm2)与两动点运动的时间![]() (s)的函数图象大致是( )
(s)的函数图象大致是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系,O为坐标原点,点A(﹣1,0),点B(0,![]() ).
).
(1)求∠BAO的度数;
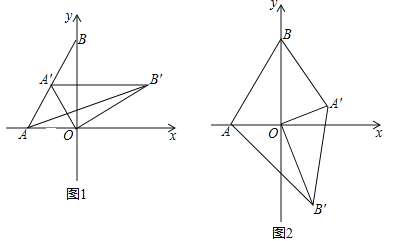
(2)如图1,将△AOB绕点O顺时针得△A′OB′,当A′恰好落在AB边上时,设△AB′O的面积为S1,△BA′O的面积为S2,S1与S2有何关系?为什么?
(3)若将△AOB绕点O顺时针旋转到如图2所示的位置,S1与S2的关系发生变化了吗?证明你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.
(1)这两次各购进这种衬衫多少件?
(2)若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于2100元,则第二批衬衫每件至少要售多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教师节当天,出租车司机小王在东西向的街道上免费接送教师,规定向东为正,向西为负,当天出租车的行程如下(单位:千米)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)将最后一名老师送到目的地时,小王距出发地多少千米?
(2)若汽车耗油量为0.5升/千米,则当天耗油多少升?若汽油价格为6.70元/升,则小王共花费了多少元钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:我们知道![]() 的几何意义是在数轴上数
的几何意义是在数轴上数![]() 对应的点与原点的距离,即
对应的点与原点的距离,即![]() ,也就是说,
,也就是说,![]() 表示在数轴上数
表示在数轴上数![]() 与数
与数![]() 对应点之间的距离.这个结论可以推广为:
对应点之间的距离.这个结论可以推广为:![]() 表示在数轴上数
表示在数轴上数![]() 与
与![]() 对应点之间的距离.
对应点之间的距离.
例![]() 已知
已知![]() ,求
,求![]() 的值.
的值.
解:在数轴上与原点距离为![]() 的点的对应数为
的点的对应数为![]() 和
和![]() ,即
,即![]() 的值为
的值为![]() 和
和![]() .
.
例![]() 已知
已知![]() ,求
,求![]() 的值.
的值.
解:在数轴上与![]() 的距离为
的距离为![]() 点的对应数为
点的对应数为![]() 和
和![]() ,即
,即![]() 的值为
的值为![]() 和
和![]() .
.
仿照阅读材料的解法,解决下列问题:
(1)已知![]() ,求
,求![]() 的值;
的值;
(2)已知![]() ,求
,求![]() 的值;
的值;
(3)若数轴上表示![]() 的点在
的点在![]() 与
与![]() 之间,则
之间,则![]() 的值为_________;
的值为_________;
(4)当![]() 满足_________时,则
满足_________时,则![]() 的值最小,最小值是_________.
的值最小,最小值是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
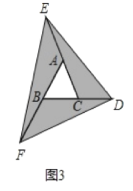
【题目】阅读理解,并完成填空:在图1至图3中,己知![]() 的面积为
的面积为![]() .
.
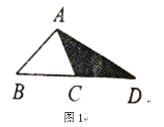
(1)如图1,延长![]() C的边
C的边![]() 到点
到点![]() ,使
,使![]() ,连结
,连结![]() .若
.若![]() 的面积为
的面积为![]() ,则
,则![]() __________(用含
__________(用含![]() 的代数式表示);
的代数式表示);
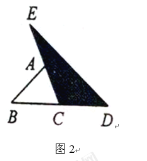
(2)如图2,延长![]() 的边
的边![]() 到点
到点![]() ,延长边
,延长边![]() 到点
到点![]() ,使
,使![]() ,
,![]() ,连结
,连结![]() ,若
,若![]() 的面积为
的面积为![]() ,则
,则![]() __________(用含
__________(用含![]() 的代数式表示);
的代数式表示);
(3)在图2的基础上延长AB到点F,使BF=AB,连接FD,得到△DEF(如图3),若阴影部分的面积为S3,则S3=___(用含a的代数式表示)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第15次“移位”后,则他所处顶点的编号为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
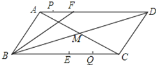
【题目】如图,![]() 中,点E是BC的中点,点F在AD上,AF=6cm,BF=12cm,BD平分∠FBC,若点P,Q分别是AF,BC上点,且CQ=2AP.若点P、Q、E、F为顶点的四边形构成平行四边形,则AP的长为______.
中,点E是BC的中点,点F在AD上,AF=6cm,BF=12cm,BD平分∠FBC,若点P,Q分别是AF,BC上点,且CQ=2AP.若点P、Q、E、F为顶点的四边形构成平行四边形,则AP的长为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com