
 直线l经过(2,3)和(-2,-1)两点,它还与x轴交于A点,与y轴交于C点,与经过原点的直线OB交于第三象限的B点,且∠ABO=30°.求:
直线l经过(2,3)和(-2,-1)两点,它还与x轴交于A点,与y轴交于C点,与经过原点的直线OB交于第三象限的B点,且∠ABO=30°.求:分析 (1)用待定系数法求出AC的解析式,分别求出点A、C的坐标即可;
(2)根据勾股定理求出AC的长,作OD⊥AC于D,BF⊥y轴于F,求出OF、BF的长即可.
解答 解:(1)设直线l的解析式为:y=kx+b,
则$\left\{\begin{array}{l}{2k+b=3}\\{-2k+b=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
∴直线l的解析式为:y=x+1,
则点A的坐标(-1,0),B(0,1).
(2)作OD⊥AC于D,BF⊥y轴于F,
∵OA=1,OC=1,
∴AC=$\sqrt{2}$,
则OD=AD=CD=$\frac{\sqrt{2}}{2}$,
在Rt△BOD中,∠ABO=30°,
BD=$\frac{\sqrt{6}}{2}$,则BC=$\frac{\sqrt{6}+\sqrt{2}}{2}$,
|BF|=|CF|=$\frac{\sqrt{2}}{2}$•$\frac{\sqrt{6}+\sqrt{2}}{2}$=$\frac{\sqrt{3}+1}{2}$,
|OF|=$\frac{\sqrt{3}+1}{2}$-1=$\frac{\sqrt{3}-1}{2}$,
∵B在第三象限,
∴点B的坐标为:(-$\frac{\sqrt{3}+1}{2}$,-$\frac{\sqrt{3}-1}{2}$).
点评 本题考查的是一次函数的知识,正确运用勾股定理和待定系数法求解析式是解题的关键,解答时,注意锐角三角函数的运用.


科目:初中数学 来源: 题型:选择题
| A. | (x+3)(x-3)=x2-9 | B. | x2-4+3x=(x+2)(x-2)+3x | ||
| C. | (x-1)2=x2-2x+1 | D. | xy2-x2y=xy(y-x) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,则下列结论:①△ABF≌△CAE;②∠AHC=120°;③△AEH∽△CEA;④AE•AD=AH•AF;其中结论正确的个数是( )
如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,则下列结论:①△ABF≌△CAE;②∠AHC=120°;③△AEH∽△CEA;④AE•AD=AH•AF;其中结论正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点P在半径为3的⊙O内,OP=$\sqrt{3}$,点A为⊙O上一动点,弦AB过点P,则AB最长为6,AB最短为2$\sqrt{6}$.
如图,点P在半径为3的⊙O内,OP=$\sqrt{3}$,点A为⊙O上一动点,弦AB过点P,则AB最长为6,AB最短为2$\sqrt{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 15 | B. | 16 | C. | 17 | D. | 18 |
查看答案和解析>>
科目:初中数学 来源:2017届福建省仙游县郊尾、枫亭五校教研小片区九年级下学期第一次月考数学试卷(解析版) 题型:单选题
要使式子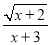 在实数范围内有意义,则x的取值范围是( )
在实数范围内有意义,则x的取值范围是( )
A.  B.
B. 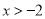 C.
C. 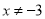 D. 以上都不对
D. 以上都不对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com